Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas Fundamentais - Ex. 6
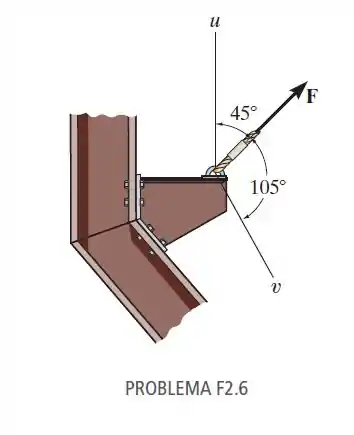
2.6. Se a força F precisa ter uma componente ao longo do eixo u com , determine a intensidade de F e de sua componente ao longo do eixo v.
Passo 1
Falaaa... tudo benzinho???
Nessa questão vamos já começar tomar um pouco de cuidado porque a gente pode pensar: “ahh... é só decompor as forças e tananana”, maaaaas repara que não temos triângulos retângulos =/
O que nos resta é montar o paralelogramo direitinho:
Passo 2
Hmmmm... como é um paralelogramo a gente tem os ângulos na pontinha do também, certo?
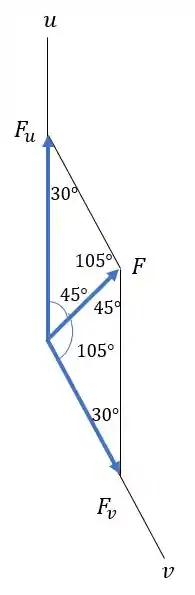
Então agora a gente pode brincar com a lei dos senos (que é o “lado” sobre o “ângulo que ta apontado pra ele”), já que os dois triângulos do paralelogramo são congruentes.
Passo 3
Então podemos resolver de boinha:
- Pra achar o :
- Pra achar o :
E acabamooos... Vamos pra próxima questão??? Só bora