Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 7.Problemas - Ex. 37
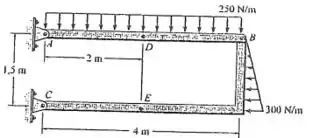
Determine a força normal interna, o esforço cortante e o momento no ponto da estrutura com dois membros.
Passo 1
Para determinar o que se pede, deve-se fazer o diagrama de corpo livre da viga para que seja possível determinar alguma reação externa ao apoio da viga. Após isso, deve-se seccionar o corpo nos pontos de referência e fazer a análise dessas seções, ou seja, fazer a análise das reações internas do sistema.
Para este caso o que pode ser feito é analisar alguma seção que envolva o ponto por ser o ponto de referência.
Uma sugestão seria fazer o DCL da seção e, assim, seria necessário determinar as reações no ponto também.
Passo 2
Então, primeiramente pode-se fazer o DCL da seção para conseguir determinar uma das reações de tal que:
Deve-se lembrar que o carregamento retangular gera uma força resultante dada por:
E a posição do seu centroide é dada por:
Com isso, supondo que o momento é positivo no sentido horário, pode-se fazer o momento em relação ao ponto e obter:
Passo 3
Agora, fazendo o DCL da seção para conseguir determinar outra reação de tem-se que:
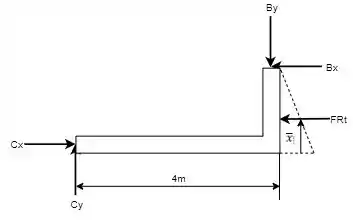
Deve-se lembrar que o carregamento triangular gera uma força resultante dada por:
E a posição do seu centroide é dada por:
Com isso, supondo que o momento é positivo no sentido horário, pode-se fazer o momento em relação ao ponto e obter:
Passo 4
Enfim, com as reações em determinadas é possível fazer o DCL da seção e encontrar os resultados desejados. Portanto:
Com isso, é possível montar as equações de equilíbrio.
Tem-se, então, para o eixo :
Para o eixo será dado por:
E, por fim, fazendo o momento em relação ao ponto de referência e supondo novamente que o momento é positivo no sentido anti-horário: