Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 12
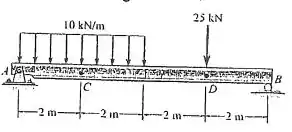
Determine a força normal interna, o esforço cortante e o momento nos pontos e da viga. O ponto está localizado à direita da carga de .
Passo 1
Fala, querido! Para resolver esse tipo de questão tem um passo a passo. Só seguir que dá bom:
- Fazer DCL
- Achar reações nos apoios
- seccionar o corpo nos pontos de referência e fazer a análise dessas seções, ou seja, fazer a análise das reações internas de cada membro seccionado.
E o que é legal é que essa análise é feita com as querinhas equações de equilíbrio. Bora lá!
Passo 2
O DCL da viga é dada por:
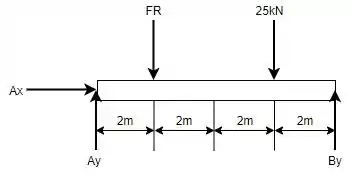
Repara que a gente substituiu a carga ditribuida por uma pontual equivalente, que vamos chamar de resultante desse carregamento. Como o carregamento é retangular, tem-se que a resultante é dada por:
E a sua posição de atuação será a mesma que a posição do seu centroide para este caso e é dada por:
Passo 3
Agora, tendo apenas as reações indeterminadas é possível determinar a reação em aplicando o somatório de momentos em relação ao ponto e supondo que o momento é positivo no sentido anti-horário, tal que:
E fazendo o somatório das forças no eixo :
E agora no eixo :
Passo 4
Então, pode-se fazer um “corte” no ponto , olhar só para um dos lados da viga e posicionar as componentes das cargas internas nessa seção.
Logo, fazendo o DCL da seção à esquerda do ponto e mostrando as forças e reações aplicadas, tem-se que:
Como o comprimento da seção diminuiu, o valor da força resultante gerada pela carga distribuída é alterado. Com isso, a força resultante gerada pela carga seccionada será:
E o seu ponto de ação será:
Passo 5
Então, voltando ao DCL da seção e aplicando as equações de equilíbrio obtém-se para o eixo :
Para o eixo :
E, aplicando o princípio dos momentos em relação ao ponto e considerando o sentido anti-horário como sendo positivo:
Passo 6
Por fim, fazendo o mesmo processo para o ponto , secciona-se a viga neste ponto e obtém-se o DCL desse membro:
Como foi mencionado no enunciado, o ponto se encontra a direita da força de e por isso, essa força estará presente no diagrama acima, beleza?
Feito isso, pode-se aplicar as equações de equilíbrio, tal que obtém-se para o eixo :
Para o eixo :
E, aplicando o princípio dos momentos em relação ao ponto e considerando o sentido anti-horário como sendo positivo:
O sinal negativo indica que a força age no sentido oposto. Logo, o esforço cortante atua para cima.