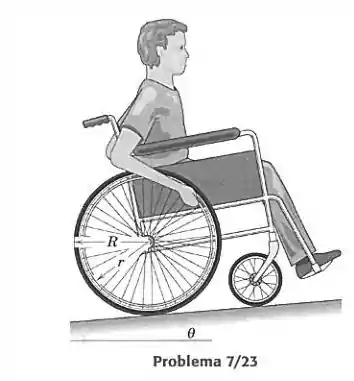
Determine a força F que a pessoa deve aplicar, tangente ao aro da roda de uma cadeira de rodas, para subir uma rampa inclinada de ângulo θ . A massa combinada da cadeira e da pessoa é m . (Se s é o deslocamento do centro da roda medido ao longo do plano inclinado e β é o ângulo correspondente, em radianos, que a roda gira, pode-se facilmente mostrar que s = R β se a roda gira sem escorregar.)

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 7.Problemas - Ex. 20

Determine a força que a pessoa deve aplicar, tangente ao aro da roda de uma cadeira de rodas, para subir uma rampa inclinada de ângulo . A massa combinada da cadeira e da pessoa é . (Se é o deslocamento do centro da roda medido ao longo do plano inclinado e é o ângulo correspondente, em radianos, que a roda gira, pode-se facilmente mostrar que se a roda gira sem escorregar.)

Passo 1

Utilizando o Princípio do Trabalho Virtual, se o sistema está em equilíbrio o trabalho virtual total realizado pelas forças externas ativas para um deslocamento pequeno do sistema deve ser zero:

Os nossos agentes externos ativos (que realizam trabalho em um deslocamento do sistema) são o peso do homem e da cadeira e o atrito que atua na roda, feito pelo chão. A força normal não realiza trabalho, por ser perpendicular ao movimento. Vamos relacionar o trabalho infinitesimal realizado pelas forças para um giro pequeno da roda, e então aplicar o princípio.

Passo 2

Primeiro vamos calcular o trabalho feito pela força de atrito na roda. No limiar do giro da roda (ainda no equilíbrio), o homem causa um momento em torno do centro da roda dado por , pois o raio do aro é . Pelo equilíbrio da roda, o momento causado pelo atrito do chão deve ter o mesmo módulo. Durante um giro da roda, a força de atrito realiza um então um trabalho:

O valor é positivo pois o momento causado pelo atrito é no sentido horário, assim como o giro da roda.

Passo 3

Agora calculamos o momento realizado pela força peso do sistema homem-cadeira. Para um giro da roda, a cadeira irá se deslocar no plano uma distância . Então sua variação de altura será:

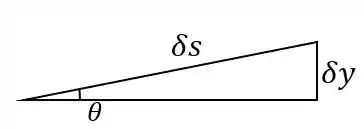
O trabalho realizado pelo peso quando levanta-se a massa de uma altura é:

O valor é negativo pois o desolcamento é para cima e a força para baixo. Então:

Passo 4

Pelo Princípio do Trabalho Virtual, temos então:

Cortando , chegamos ao valor de :

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma plataforma de carga elétrica projetada para a parte traseira de um caminhão é mostrada na figura. A posição da plataforma é controlada pelo cilindro hidráulico, que aplica força em C. Os links são

Resolva o problema 17.25, assumindo que o cilindro é substituído por um tubo de parede fina de raio r e massa m.17.25 - Uma corda é enrolada em torno de um cilindro de raio r e massa m, conforme mostr

Cada um dos elos uniformes idênticos tem um comprimento le uma massa me está sujeito a um par M, um no sentido horário e outro no sentido anti-horário, aplicado como mostrado. Determine o ângulo que c

Determine a força N exercida na tora por cada mandíbula das pinças para lareira mostradas.

Determine a força F entre as mandíbulas da braçadeira em termos de um torque M exercido na alça do parafuso de ajuste. O parafuso tem avanço (avanço por rotação) L e o atrito deve ser desprezado.