Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 31
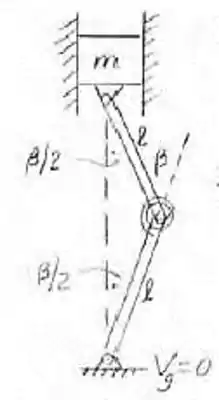
Cada um dos elos uniformes idênticos tem um comprimento le uma massa me está sujeito a um par M, um no sentido horário e outro no sentido anti-horário, aplicado como mostrado. Determine o ângulo que cada elo faz com a horizontal quando o sistema está em sua configuração de equilíbrio.
Passo 1
O enunciado pede que a gente determine o ângulo que cada elo faz com a horizontal quando o sistema está em sua configuração de equilíbrio
Passo 2
Resposta
Exercícios de Livros Relacionados
A mola conectada ao mecanismo não tem deformação quando θ = 90 ° . Determine a posição θ para haver equilíbrio e investigue a estabilidade do mecanismo nessa posição. O disco A é conectado por pino à
A haste uniforme A B tem massa de 50k g . Se as duas molas D E e B C não estão deformadas quando θ = 90 ° , determine o ângulo θ para haver equilíbrio usando o princípio da energia potencial. Investig
A haste uniforme A B tem massa de 5k g . Se a mola conectada não está deformada quando θ = 90 ° , determine o ângulo θ de equilíbrio usando o método do trabalho virtual. Observe que a mola sempre perm
Os elementos uniformes A B e B C possuem massa de 1k g cada e o cilindro possui 10k g . Determine a força horizontal P necessária para manter o mecanismo em posição quando θ = 45 ° . A mola tem compri
Para o mecanismo mostrado, a mola de rigidez k tem um comprimento não alongado de essencialmente zero, e o elo maior tem uma massa m com centro de massa em B. A massa do elo menor é desprezível. Deter