Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 7.Problemas - Ex. 24

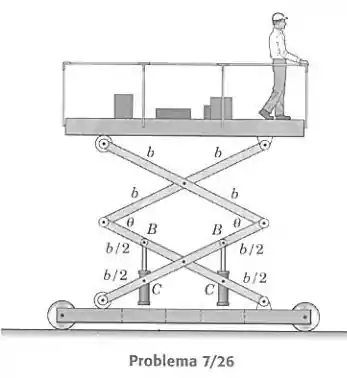
A plataforma de trabalho portátil é elevada por intermédio de dois cilindros hidráulicos articulados nos pontos C . Cada cilindro está sob uma pressão hidráulica p e tem uma área de pistão A . Determine a pressão p necessária para sustentar a plataforma e mostre que ela é independente de θ . A plataforma, o trabalhador e os suprimentos têm uma massa combinada m e as massas das barras de conexão podem ser desprezadas.

Passo 1

Utilizando o Princípio do Trabalho Virtual, se o sistema está em equilíbrio o trabalho virtual δ U total realizado pelas forças externas ativas (forças que realizam trabalho) para um deslocamento pequeno do sistema deve ser zero:

δ U = 0

Os nossos agentes externos ativos são o peso m g da plataforma com o trabalhador e os suprimentos e as forças nos cilindros hirdáulicos . As forças nos apoios não realizam trabalho, pois ou o apoio é fixo ou a força feita nele é perpendicular ao movimento permitido naquele ponto. Vamos calcular então o trabalho virtual realizado pelo peso m g e pela força nos cilindros para uma pequena variação δ θ da angulação das barras, e então aplicar o princípio.

Passo 2

Primeiro calculamos o trabalho δ U 1 feito pelo peso da plataforma para uma variação δ θ . A altura y G do centro de massa do conjunto plataforma-homem-suprimentos em relação ao solo é dada por uma constante fixa c mais 4 b sen ⁡ θ 2 .

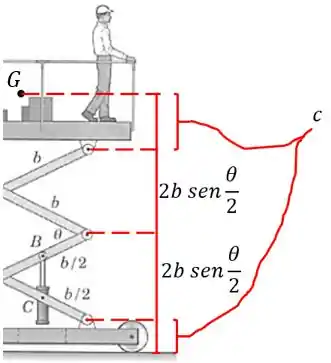
Derivando a expressão da altura y G , achamos o deslocamento δ y G para um deslocamento δ θ do ângulo:

y G = c + 4 b sen ⁡ θ 2

δ y G = 2 b cos ⁡ θ 2 δ θ

Então o trabalho realizado pelo peso é:

δ U 1 = - m g   δ y G = - 2 m g b cos ⁡ θ 2 δ θ

Passo 3

Agora calculamos o trabalho δ U 2 realizado pelos cilindros. Os pontos C tem uma altura dada por um valor fixo d mais b 2 sen ⁡ θ 2 . Os pontos B tem altura dada pelo mesmo valor fixo d mais 3 b 2 sen ⁡ θ 2 :

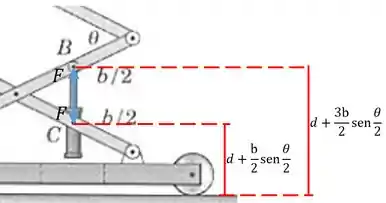
A variação das alturas de B e C em função de δ θ são obtidas por derivação:

δ y B = 3 b 2 1 2 cos ⁡ θ 2 δ θ = 3 b 4 cos ⁡ θ 2 δ θ

δ y C = b 2 1 2 cos ⁡ θ 2 δ θ = b 4 cos ⁡ θ 2 δ θ

O trabalho realizado por cada cilindro é então:

F   δ y B - F   δ y C = F ( δ y B - δ y C )

O segundo valor é negativo pois a força é para baixo e o deslocamento para cima. Para achar então δ U 2 , substituímos F por p A e multiplicamos por 2 pois são dois cilindros:

δ U 2 = 2 p A 3 b 4 cos ⁡ θ 2 δ θ - b 4 cos ⁡ θ 2 δ θ

= 2 p A 2 b 4 cos ⁡ θ 2 δ θ = 2 p A b cos ⁡ θ 2 δ θ

Passo 4

Pelo Princípio do Trabalho Virtual, temos então:

δ U = δ U 1 + δ U 2 = 0

⇒ - 2 m g b cos ⁡ θ 2 δ θ + 2 p A b cos ⁡ θ 2 δ θ = 0

⇒ 2 m g b cos ⁡ θ 2 δ θ = 2 p A b cos ⁡ θ 2 δ θ

Cortando b cos ⁡ θ 2 δ θ , chegamos ao valor de p :

2 m g = 2 p A

p = m g A

Vemos que esse valor de fato não depende de θ .

Resposta

p = m g A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

32- Uma chave de boca antitorque é projetada para ser usada por um tripulante de uma nave espacial onde ele não tem uma plataforma estável contra a qual se empurrar enquanto aperta um parafuso. O pino
31- Determine a força N exercida na tora por cada garra do pegador de lenha mostrado.
33- Uma plataforma automática de carga, projetada para a traseira de um caminhão, está mostrada na figura. A posição da plataforma é controlada pelo cilindro hidráulico, que aplica força em C . As con
68- A figura mostra a vista lateral de uma claraboia uniforme de massa m e com centro de massa na metade da distância entre A e O . A clarabóia é contrabalançada pela ação da mola, que tem uma rigidez
73- Os roletes nas extremidades da barra uniforme A B , de 10k g , se movem livremente nas guias horizontal e vertical, como mostrado. Determine a posição de equilíbrio θ para a barra sob a ação de um