Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 57

Determine a força resultante que as tensões de flexão produzem na tábua superior A da viga se M   =   1,5   k N . m .

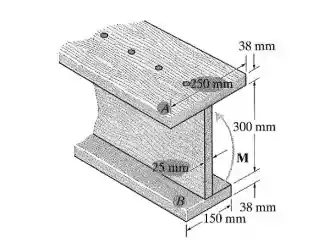
Passo 1

Primeiro, vamos determinar a coordenada y do centróide:

y = 38 × 150 × 19 + 300 × 25 × 188 + 250 × 38 × 357 150 × 38 + 300 × 25 + 250 × 38 = 216,2907 m m

Agora, podemos calcular o momento de inércia:

I = 0,15 × 0,038 3 12 + 0,15 × 0,038 × 0,1973 2 + 0,025 × 0,3 3 12 + 0,025 × 0,3 × 0,0283 2 + 0,025 × 0,038 3 12 + 0,025 × 0,038 × 0,1407 2

I = 4,74038 × 10 - 4 m 4

Com isso, podemos calcular as tensões máximas e mínimas em A:

σ a m á x = 1,5 × 10 3 0,376 - 0,2162907 4,74038 × 10 - 4 = 0,5054 M P a

σ a m i n = 1,5 × 10 3 0,338 - 0,2162907 4,74038 × 10 - 4 = 0,3851 M P a

Passo 2

Logo, a força resultante será dada por:

F r a = 0,5054 + 0,3851 10 6 0,038 × 0,25 2 = 4,23 k N

Resposta

F r a = 4,23 k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Trace os diagramas de força cortante e o momento fletor para a viga e carregamento mostrados, e determine o valor máximo absoluto ( a ) da força cortante e momento fletor e ( b ) do momento fletor.
Para a viga e o carregamento mostrados, determine a tensão normal máxima provocada pelo momento fletor na seção transversal C .
Para a viga e o carregamento mostrados, determine a tensão normal máxima provocada pelo momento fletor na seção transversal C .
Para a viga e o carregamento mostrados, determine a tensão normal máxima provocada pelo momento fletor na seção transversal C .
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados na figura, e determine a tensão normal máxima gerada pelo momento fletor.