Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 27
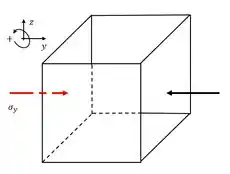
Resolva o Problema para o ponto .
Passo 1
Uma barra engastada a uma parede sofre um carregamento de na extremidade livre.
A barra tem diâmetro .
Queremos saber como ficam as tensões em um ponto que está a da extremidade livre.
Vamos achar primeiro as forças e momentos internos na seção transversal que passam por . Aí podemos calcular as tensões e desenhar o elemento de volume nesse ponto.
Passo 2
Vamos ver como ficam as forças. Diagrama de corpo livre:
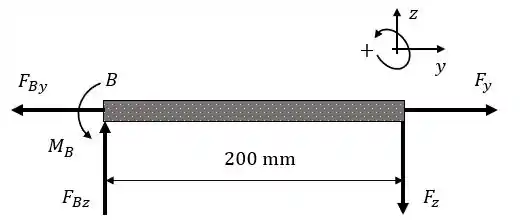
As componentes do carregamento são:
Checando cada equilíbrio, podemos saber como fica a força interna e o momento interno na seção que passa em .
Tranquilo! Agora vamos pensar qual o efeito que cada esforço faz na seção.
- A força causa tração:
- A força causa cisalhamento na direção positiva . Mas o ponto está na borda da seção. Como o não há carregamento na superfície externa, não podemos ter cisalhamento nesse ponto para direção , senão não tem como equilibrar!
- O momento causa flexão, que vai gerar tração em e compressão em .
Então temos todas as fórmulas para usar. Vamos calcular com calma cada propriedade dessa seção pro ponto e aí voltamos pra fechar as contas!
Passo 3
Área da seção (círculo):
Segundo momento de área (círculo, em relação ao eixo neutro):
A distância do ponto para o eixo neutro é
Show! Finalmente vamos calcular as tensões!
Passo 4
Vejamos uma direção de cada vez.
Na direção não temos tensões nesse problema.
Na direção , temos a tração gerada pela força :
E também na direção , temos a compressão gerada por (ponto está abaixo do eixo neutro):
Somando os efeitos:
A tensão causa compressão no ponto !
Passo 5
Só falta desenhar. Confira bem qual é a seção que você está tratando (Passo ), e trace as tensões pro ponto pelo o que você descobriu no Passo . Aí é só fazer as outras setas pensando no equilíbrio!
A seta vermelha atua no plano da seção considerada.
Resposta
Compressão no ponto :
