Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 88

Determine a inclinação em B e o deslocamento em C. O elemento é um T estrutural de aço A-36 para o qual I = 30 × 10 6 m m 4 .

Passo 1

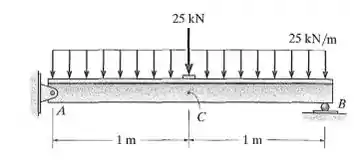
Fala aí galera, partiu resolver outra questão de resmat. O primeiro passo nessa questão é determinar a equação do momento. Para isso, basta vir caminhando com a coordenada x pela viga somando ou diminuindo as parcelas dos momentos causadas pelas forças. Como nosso foco aqui não é determinar reações de apoio e existe um capítulo do livro só pra isso, vamos direto para a equação do momento:

M x = 37,5 x - 12,5 x ² - 25 < x - 1 >

Caso tenham dúvida nos valores, basta aplicar as equações de equilíbrio.  

Sabemos que a equação da linha neutra é:

E I d 2 v d x 2 = M x

Logo, integrando 2 vezes os dois lados da equação, teremos:

E I v = 6,25 x ³ - 1,04 x 4 - 4,16 < x - 1 > ³ + C 1 x + C 2

Para determinar as constantes, vamos aplicar as condições de contorno:

x = 0 → v = 0

x = 2 → v = 0

Aplicando as condições e resolvendo o sistema:

C 1 = - 14,58

C 2 = 0

Passo 2

A inclinação em B ocorre em:

x = 2

Logo, ela será:

θ b = 0,00243 r a d

A deflexão em C ( x = 1 ) será:

∆ c = 1,56 m m  

Resposta

θ b = 0,00243 r a d

∆ c = 1,56 m m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um macaco hidráulico pode ser usado para levantar o ponto B, de uma viga em balanço ABC. Sabendo-se que, depois da carga de 20kN ser aplicada, o ponto C deve estar no mesmo nível do ponto A, determina
Para a viga com o carregamento do Prob.9.95, determinar:Quanto o ponto B deverá ser levantado, se a deflexão em CF deve ser de 10mm para baixo, em relação à horizontal que passa por A;A reação em B de
Para a viga com o carregamento mostrado, determinar a constante de mola k para que o momento fletor em B seja M B = - w L 2 / 12 .
Para a viga com o carregamento do Prob.9.95, determinar:Quanto o ponto B deverá ser levantado, se a deflexão em CF deve ser de 10mm para baixo, em relação à horizontal que passa por A;A reação em B de
Para a viga com o carregamento mostrado, determinar:O valor de a para que a declividade na extremidade A seja zero;A correspondente deflexão no ponto C.