Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 39
Determine por integração direta o centroide da área mostrada na figura.
Passo 1
Fala aí galera, vamos pra mais um problema de estática. O problema quer que a gente determine o centroide por integração. Para isso, Sabemos que:
Agora, precisamos determinar o termo , que nada mais é do que a área da nossa figura que está variando:
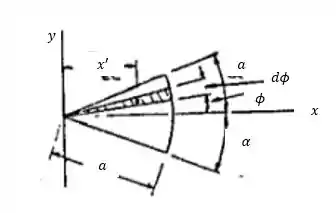
Para a área, vamos integrar o termo . Fica assim:
Passo 2
Agora, para encontrarmos os centroides, devemos utilizar as seguintes fórmulas:
Como já temos a integral de , vamos calcular as integrais do numerador:
Passo 3
Por fim, basta substituirmos o numerador e o denominador, ficaremos com:
Vale ressaltar que o nosso foco não é nas operações matemáticas.
Resposta
Exercícios de Livros Relacionados
Para o mecanismo do problema indicado nas figuras, determine a aceleração do colar B.
O corpo mostrado em seção transversal é um anel circular completo formado pela rotação da área octogonal em torno do eixo z. Toda a superfície deve ser coberta com um revestimento especial. Determine
Para o mecanismo do problema indicado nas figuras, determine a aceleração do colar A.
Para o mecanismo do problema indicado nas figuras, determine a aceleração do colar A.
Determine as coordenadas do centro de massa do corpo construído em chapa de aço e uma barra de aço. A espessura da placa é de 2 mm. O diâmetro da haste é de 4 mm e seu comprimento é de 50 mm. A origem