Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 31

Determine o valor do ângulo θ para que a estrutura esteja em equilíbrio:

Passo 1

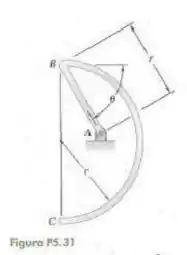
Fala aí galera, vamos pra mais um problema de estática. Para que a estrutura esteja em equilíbrio, precisamos que o ponto A seja o centroide da estrutura. Logo:

L × x - 1 = r × - r c o s θ 2 = - r 2 c o s θ 2

L × x - 2 = π r × ( - cos ⁡ θ r + r / 2 )

Logo:

x - =   - r 2 c o s θ 2 + π r × ( - cos ⁡ θ r + r / 2 ) r + π r

Para que o ponto A esteja no centroide, a coordenada do ponto deve ser 0, logo:

0 =   - r 2 c o s θ 2 + π r × ( - cos ⁡ θ r + r / 2 ) r + π r

r 2 c o s θ 2 = - π r 2 cos ⁡ θ + r 2 π 2

cos ⁡ θ r 2 2 + π r 2 = r 2 π 2

cos ⁡ θ 2 π r 2 + r 2 2 = r 2 π 2

cos ⁡ θ = r 2 π 2 π r 2 + r 2

cos ⁡ θ = π 2 π + 1 = 0,431

θ = 64,44 º

Resposta

θ = 64,44 º

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o centroide da área a seguir:
Calcule o centroide da área a seguir:
Calcule o centroide da área a seguir:
Calcule o centroide da área a seguir:
Calcule o centroide da área a seguir: