Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 30

Sabendo que d = 0 , 5 m   determine o comprimento l tal que a parte B C D seja horizontal:

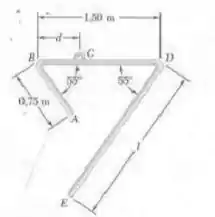
Passo 1

Fala aí galera, vamos pra mais um problema de estática. Para que a parte B C D   seja horizontal, C deve estar na coordenada x do centroide da peça, ou seja, x - = 0,5 . Logo:

L × x - 1 = 0,75 × 0,215 = 0,161

L × x - 2 = 1,5 × 0,75 = 1,125

L × x - 3 = 1,5 - cos ⁡ 55 l 2 × l

Logo, o centroide da figura será:

x - = 0,161 + 1,125 + 1,5 - cos ⁡ 55 l 2 × l 0,75 + 1,5 + l = 1,286 + 1,5 l - 0,286 l 2 2,25 + l

Logo:

0,5 = 1,286 + 1,5 l - 0,286 l 2 2,25 + l

1,125 + 0,5 l = 1,286 + 1,5 l - 0,286 l 2

0,161 + l - 0,286 l 2 = 0

Portanto:

∆ = 1 + 0,184 = 1,184

l = - 1 ± 1,08 8 - 0,572

Como l   não pode ser negativo:

l = 3,65 m  

Resposta

l = 3,65 m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que l = 2 m , determine a distância d tal que a parte B C D seja horizontal:
Se a distância h foi escolhida de modo a maximizar y - , mostre que y - = 2 h 3 .
Determine as coordenadas do centroide por integração em termos de a e h :
Determine a distância h para a qual o centroide da área sombreada fique o mais distante de BB’, quando (a) k = 0,1 eb k = 0,8 .
Determine as coordenadas do centroide por integração em termos de a e h :