Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 92

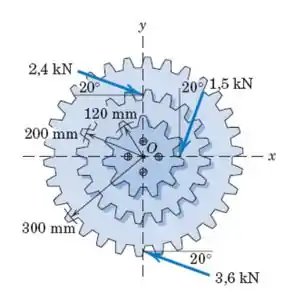
Determine as interseções  x   e   y  da linha de ação da resultante dos três carregamentos aplicados ao conjunto de engrenagens.

Passo 1

E aí meus queridxs, tudo bem com vocês?

Se liguem só que essa questão exige um pouco de atenção, mas nada que a gente não seja capaz de fazer. Primeiro de tudo vamos calcular a resultante em cada uma das direções que serão dadas por

R x = ∑ f x = 2,4 ⋅ cos ⁡ 20 ° - 3,6 ⋅ cos ⁡ 20 ° - 1,5 ⋅ s e n 20 ° ≈ - 1,64   k N

R x = ∑ f x = 2,4 ⋅ s en ⁡ 20 ° - 3,6 ⋅ s en ⁡ 20 ° - 1,5 ⋅ c o s 20 ° ≈ - 1   k N

Assim, nosso vetor resultante será

R = R x   i ^ + R y   j ^ = - 1,64   i ^ - 1 j ^   k N

Passo 2

Agora calculando o momento em relação ao ponto O , adotando o sentido anti horário como positivo, vamos ter

M O = - 2,4 ⋅ cos ⁡ 20 ° ⋅ 0,2 + 2,4 ⋅ s en ⁡ 20 ° ⋅ 0,2 - 3 , 6 ⋅ cos ⁡ 20 ° ⋅ 0 , 3 + 3 , 6 ⋅ sen ⁡ 20 ° ⋅ 0 , 3 - 1,5 ⋅ cos ⁡ 20 ° ⋅ 0 , 1 2 + 1 , 5 ⋅ sen ⁡ 20 ° ⋅ 0 , 1 2

M 0 = - 1,637   k N ⋅ m = - 1,637   k ^   k N ⋅ m

Passo 3

Pronto, nosso problema está quase resolvido resta-nos encontrar a equação que descreve a linha de ação da força para encontramos o ponto de intersecção com os eixos. Para isso, vamos fazer o seguinte

x   i ^ + y   j ^ × - 1,64   i ^ - 1 j ^ = M O

- x   k ^ + 1,64 ⋅ y   k ^ k N ⋅ m = - 1,637   k ^   k N ⋅ m

- x   + 1,64 ⋅ y   = - 1,637  

Para encontrar a interseção com o eixo y faremos x = 0 então

1,64 y = - 1,637 → y ≈ 0,998 m

Por fim, a interseção com o eixo x será dada quando y = 0 então

- x = - 1,637 → x = 1,637   m

Protinho tá resolvido nosso problema.

Resposta

x = 1,637 m   ,     y = - 0,998   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O pedal da roda dentada de uma bicicleta é mostrado na figura. O pé esquerdo do ciclista exerce uma força de 160N , enquanto o uso da ponta do dedo do pé direito exerce uma força ascendente de quase 8
A viga de aço em balanço, com flanges e suportes rebitados, é submetida ao binário das duas forças mostradas e seus efeitos sobre a ligação em A devem ser determinados. Substitua as duas forças e o bi
O comprimento não esticado da mola é b . Determinar a força que a mola exerce sobre o ponto B da armação se b=0,3m . O módulo da força da mola é a constante da mola k multiplicado pela deflexão (por a
A treliça do tipo telhado assimétrico é usada quando é desejável, para fins de energia solar, um ângulo normal de incidência da luz solar sobre a superfície virada para o sul A B C . Os cinco carregam