Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 87

A viga de aço em balanço, com flanges e suportes rebitados, é submetida ao binário das duas forças mostradas e seus efeitos sobre a ligação em  A  devem ser determinados. Substitua as duas forças e o binário por um binário equivalente  M  e uma resultante de força  R  em  A .

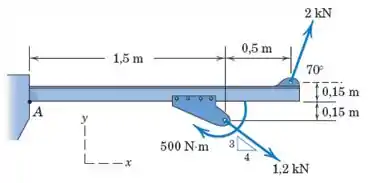
Passo 1

E aí meus queridxs, tudo bem com vocês?

Se liguem só que essa questão exige um pouco de atenção, mas nada que a gente não seja capaz de fazer. Vamos lá, primeiramente vamos decompor nossas forças adotando a seguinte notação

F o r ç a   d e   2 k N :   F x = 2000 ⋅ cos ⁡ 70 ° F y = 2000 ⋅ sin ⁡ 70 °

F o r ç a   d e   1 , 2 k N :   F x 2 = 1 200 ⋅ 4 5 F y 2 = 1 200 ⋅ 3 5

Passo 2

Pois bem, feito isso nosso problema passa a ser muito mais simples. Começaremos encontrando a resultante das forças em cada uma das direções que vai ser dada por

R x = ∑ F x = 2 k N ⋅ cos ⁡ 70 ° + 1,2 k N ⋅ 4 5 ≈ 1,644   k N

R y = ∑ F y = 2 k N ⋅ s en ⁡ 70 ° + 1,2 k N ⋅ 3 5 ≈ 1 , 159   k N

Sendo assim, nosso vetor resultante vai ser dado por

R = 1,644   i ^ + 1,159   j ^   k N

Passo 3

Para calcularmos o momento em relação ao ponto A vamos adotar o sentido anti-horário como positivo e fazer a multiplicação de cada força pela distância perpendicular em relação ao ponto que estamos calculando. Sendo assim, teremos

M A = - 500 N ⋅ m - F y 2 ⋅ 1,5 m + F y ⋅ 2 m - 0,15 m ⋅ F x + 0,15 ⋅ F x 2

M A = - 500 - 1080 + 3759 - 103 + 144   N ⋅ m

M A = 2,22   k N ⋅ M   s e n t i d o   a n t i - h o r á r i o

Pronto, tá resolvido nosso problema.

Resposta

R = 1,644   i ^ + 1,159   j ^   k N

M A = 2,22   k N ⋅ M   s e n t i d o   a n t i - h o r á r i o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Substitua as três forças que atuam na haste dobrada por um sistema força-binário equivalente no ponto A do suporte. Em seguida, determine a interseção x da linha de ação da força resultante independen
As três forças atuam perpendicular a placa retangular como mostrado. Determine os momentos M 1 deF 1 ,M 2d eF 2eM 3d eF 3 , todos relacionados ao ponto O .
A tensão no suporte do cabo B Cé3200N é . Escreva a força que este cabo exerce sobre a longarina O A B como um vetor T . Determine os ângulos θ x ,θ yeθ zque a linha de ação de T formam com os eixos p
A viga H , de aço, foi projetada como uma coluna para suportar as duas forças verticais, como mostrado. Substitua essas forças por uma força equivalente simples ao longo da linha de centro vertical da
O tensionador é apertado até que a força trativa no cabo A B seja de 1,2k N . Calcule a magnitude do módulo em relação ao ponto O da força atuando no ponto A .