Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 100
O pedal da roda dentada de uma bicicleta é mostrado na figura. O pé esquerdo do ciclista exerce uma força de , enquanto o uso da ponta do dedo do pé direito exerce uma força ascendente de quase . Determine o sistema força-binário no ponto . Determine, também, a equação da linha de ação do sistema resultante tratado como um ângulo de força . Trate o problema como bidimensional.
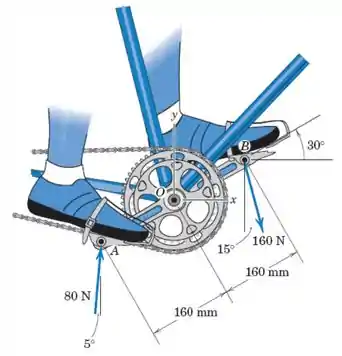
Passo 1
E aí meus queridos, tudo bom?
Então, prestem muita atenção nesse problema porque ele envolve uns detalhezinhos que podem deixar a gente confuso de não prestar bastante atenção. Primeiro de tudo, vamos calcular a nossa resultante e para isso vamos utilizar um pouco de trigonometria. Calculando cada componente da nossa resultante vamos ter
Sendo assim, nosso vetor resultante será dado por
Passo 2
Nossa força deve gerar o mesmo momento em e esse, por sua vez, vai ser dado por
Lembrando que o sinal de negativo indica que a tendência da rotação se dá no sentido horário.
Passo 3
Beleza, temos nossa resultante e o momento calculado em , agora, para finalizar o problema vamos encontrar a linha de ação da nossa força fazendo o seguinte
Isolando para encontrarmos a equação da linha de ação da força vamos ter
Pronto, tá resolvido nosso problema.