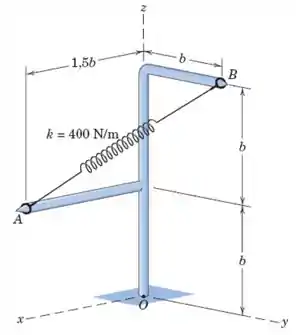
O comprimento não esticado da mola é . Determinar a força que a mola exerce sobre o ponto  da armação se . O módulo da força da mola é a constante da mola  multiplicado pela deflexão (por alongamento ou encurtamento) da mola.

E aí meus queridos, tudo bom?

Então, prestem muita atenção nesse problema porque ele envolve uns detalhezinhos que podem deixar a gente confuso de não prestar bastante atenção. Primeiramente, utilizando vamos ter o alongamento da nossa mola vai ser dado por

Onde representa a diagonal de um paralelepípedo. Com isso, conseguimos determinar o módulo da nossa força pois foi dado no enunciado que esse valor é dado multiplicando-se o alongamento pela constante elástica. Então, tomando temos

Agora, vamos pegar o vetor unitário na direção dado os pontos

Nosso vetor unitário vai ser dado por