Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 30

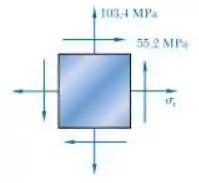
Determine o intervalo de valores de σ x para o qual a tensão de cisalhamento máxima no plano das tensões é igual ou menor que 69   M P a .

Passo 1

Fala aí, pessoal. Tudo bem certa? Bora estudar mecânica e garantir aquele notão na prova.

Este problema nos pede para determinarmos o maior valor de σ y y para o qual a tensão de cisalhamento máxima no plano das tensões é igual ou menor que 75   M P a . Para isso, sabemos que a tensão máxima é dada por:

τ m á x = R =   σ x - σ y 2 2 + τ x y 2 69 = σ x - 103,4 2 2 + ( 55,2 ) 2

Agora, basta isolarmos o a tensão de cisalhamento. Como temos uma equação do segundo grau, teremos duas tensões possíveis. Logo:

σ x = 20,7   M P a   o u   186,16   M P a

Portanto, os extremos do nosso intervalo são dados pelas tensões de cisalhamento que encontramos. Fica assim:

20,7   M P a ≤ σ x ≤ 186,16   M P a

É isso, galerinha. Bora fazer mais questões.

Resposta

20,7   M P a ≤ σ x ≤ 186,16   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o estado de tensões dado, determine as tensões normal e de cisalhamento depois que o elemento mostrado sofreu uma rotação de (a) 25 ° no sentido horário e (b) 10 ° no sentido anti-horário.
Para o estado plano de tensão mostrado, determine o maior valor de σ y para o qual a tensão de cisalhamento máxima no plano das tensões é igual ou menor que 75M P a .
As fibras de um elemento de madeira formam um ângulo de 15 ° com a vertical. Para o estado de tensão mostrado, determine (a) a tensão de cisalhamento no plano da tensão paralela às fibras e (b) a tens
Para o estado de tensões dado, determine as tensões normal e de cisalhamento depois que o elemento mostrado sofreu uma rotação de (a) 25 ° no sentido horário e (b) 10 ° no sentido anti-horário.