Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 14

Para o estado de tensões dado, determine as tensões normal e de cisalhamento depois que o elemento mostrado sofreu uma rotação de (a) 25 ° no sentido horário e (b) 10 °   no sentido anti-horário.

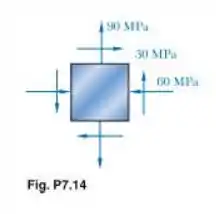
Passo 1

Fala aí, galerinha. Tudo bem com vocês? Bora fazer outra questão.

Primeiramente, sabemos que, para este caso:

σ x = - 60   M P a

σ y = 90   M P a

τ x y = 30   M P a

Também, precisamos calcular os seguintes parâmetros:

σ x + σ y 2 = 15   M P a

σ x - σ y 2 = - 75   M P a

Passo 2

Sabemos que, as tensões após a rotação serão:

σ x ' = σ x + σ y 2 + σ x - σ y 2 cos ⁡ 2 θ + τ x y   × s e n ( 2 θ )

τ x ' y ' = - σ x - σ y 2 s e n 2 θ + τ x y cos ⁡ 2 θ

σ y ' = σ x + σ y 2 - σ x - σ y 2 cos ⁡ 2 θ - τ x y s e n 2 θ

Logo, basta substituir os valores nas fórmulas. Para a letra a:

θ = - 25 °

σ x ' = - 56,2   M P a

τ x ' y ' = - 38,2   M P a

σ y ' = 86,2   M P a

Passo 3

Agora, para a letra b:

θ = 10 °

Logo:

σ x ' = - 45,2   M P a

τ x ' y ' = 53,8   M P a

σ y ' = 75,2   M P a

Resposta

  1. σ x ' = - 56,2   M P a ;   τ x ' y ' = - 38,2   M P a ;   σ y ' = 86,2   M P a
  2. σ x ' = - 45,2   M P a ;   τ x ' y ' = 53,8   M P a ;   σ y ' = 75,2   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o estado de tensões dado, determine (a) os planos principais e (b) as tensões principais.
Para o estado de tensões dado, determine as tensões normal e de cisalhamento depois que o elemento mostrado sofreu uma rotação de (a) 25 ° no sentido horário e (b) 10 ° no sentido anti-horário.
Para os estados de tensão mostrados nas figuras, determine as tensões normal e de cisalhamento que atuam na face oblíqua do elemento triangular sombreado na figura. Use um método de análise com base n
Para o estado de tensões dado, determine (a) a orientação dos planos de máxima tensão de cisalhamento no plano de tensões e (b) a tensão normal correspondente.
Para o estado de tensões dado, determine (a) a orientação dos planos de máxima tensão de cisalhamento no plano de tensões e (b) a tensão normal correspondente.