Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 18
As fibras de um elemento de madeira formam um ângulo de com a vertical. Para o estado de tensão mostrado, determine (a) a tensão de cisalhamento no plano da tensão paralela às fibras e (b) a tensão normal perpendicular às fibras.
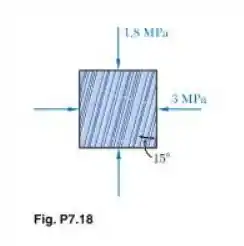
Passo 1
Fala aí, galerinha. Tudo bem com vocês? Bora pra outra questão.
Sabemos que, para este caso:
Passo 2
Agora, basta aplicar as fórmulas. Sabemos que a tensão cisalhamento é:
Já a tensão normal é dada por:
Resposta
Exercícios de Livros Relacionados
Para o estado plano de deformação dado, use o método da seção 7.10 para determinar o estado plano de deformação associado aos eixos x ' e y ' que sofreram uma rotação do ângulo θ dado.
Para o estado plano de deformação dado, use o método da seção 7.10 para determinar o estado plano de deformação associado aos eixos x ' e y ' que sofreram uma rotação do ângulo θ dado.
Para o estado plano de deformação dado, use o círculo de Mohr para determinar o estado plano de deformação associado aos eixos x ' e y ' que sofreram uma rotação do ângulo θ dado.
Para o estado plano de deformação dado, use o círculo de Mohr para determinar o estado plano de deformação associado aos eixos x ' e y ' que sofreram uma rotação do ângulo θ dado.
Para o estado plano de deformação dado, use o círculo de Mohr para determinar o estado plano de deformação associado aos eixos x ' e y ' que sofreram uma rotação do ângulo θ dado.