Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 64

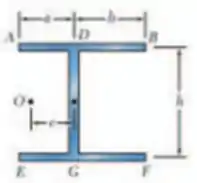
Determine a localização do centro de cisalhamento O de uma viga d paredes finas de espessura uniforme com a seção transversal mostrada.

Passo 1

E ai gurizada tudo bem? O enunciado pede que a gente determine a localização do centro de cisalhamento O de uma viga, vamos ao esboço ;)

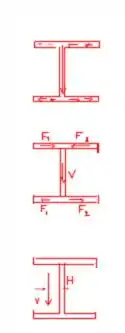
Passo 2

Agora devemos calcular a inércia :D

I A B = I E F = ( a + b ) t h 2 2 + 1 12 ( a + b ) t 3 = 1 4 t ( a + b ) h 2

I D G = 1 12 t h 3

I = Σ I = 1 12 t ( 6 a + 6 b + h ) h 2

Passo 3

Parte AD:

Q = t x h 2 = 1 2 t h x

t = V Q I t = V h x 2 I

F 1 = ∫ = t d A = ∫ 0 a V h x 2 I t   d x = V h x 2 I ∫ 0 a x d x = V h x 2 I x 2 2 ∫ 0 a = V h t a 2 4 I

Passo 4

Parte BD:

Q = t x h 2 = 1 2 t h x

t = V Q I t = V h x 2 I

F 2 = ∫ t d A = ∫ 0 b V h x 2 I t   d x = V h 2 I ∫ 0 b x d x = V h x 2 I x 2 2 ∫ 0 b = V h t b 2 4 I

Calculando os momentos temos:

Σ M H = Σ M H :

V e = F 2 h - F 1 h = V h 2 t b 2 - a 2 4 I = V h 2 t b 2 - a 2 4 ⋅ 1 12 t ( 6 a + 6 b + h ) h 2 = 3 V b 2 - a 2 6 a + 6 b + h

e = 3 ( b 2 - a 2 ) 6 ( a + b ) + h

Resposta

e = 3 ( b 2 - a 2 ) 6 ( a + b ) + h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma laje de concreto é reforçada por três barras de aço colocadas conforme mostra figura. O módulo de elasticidade é de 20,7G P a para o concreto e de 20 7G P a para o aço. usando uma tensão admissíve
A viga composta mostrada é formada colando uma haste de latão e outra de alumínio com seções transversais semicirculares. O módulo de elasticidade do latão é de 15 ×10 6p s i e do alumínio é de 10 × 1
Cinco tiras de metal, cada uma com 0,5 x 1,5i n de seção transversal, são unidas para formar uma viga composta, mostrada na figura. O modulo de elasticidade é de 30 × 10 6 p s i para o aço, de 15 × 10
Sabendo que o momento fletor em uma viga de concreto reforçado é de 100k N m e que o modulo de elasticidade é de 3,625G P a para o concreto e 29G P a para o aço, determine.A tensão no aço A tensão máx
Cinco tiras de metal, cada uma com 0,5 x 1,5i n de seção transversal, são unidas para formar uma viga composta, mostrada na figura. O modulo de elasticidade é de 30 × 10 6 p s i para o aço, de 15 × 10