Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 57

A viga composta mostrada é formada colando uma haste de latão e outra de alumínio com seções transversais semicirculares. O módulo de elasticidade do latão é de 15 ×   10 6   p s i e do alumínio é de 10 × 10 6   p s i . Sabendo que a viga composta é fletida em relação ao eixo horizontal por conjugados de 8   k i p ∙ i n , determine a tensão máxima.

  1. No latão
  2. No alumínio

Passo 1

Quando temos mais de um material na nossa barra precisamos converter todos ela para um deles para facilitar o nosso cálculo.

Sabemos que o nosso fator a ser calculado é dado por:

n = E p a r t e   t r a n s f o r m a d a   E p a r t e   i n t a c t a  

Vamos então fazer o seguinte, vamos manter como intacto o alumínio, e vamos transformar o latão, sendo assim vamos ter o seguinte fator de transformação:

n l a t ã o = E l a t ã o   E a l u m i n i o   = 15 × 10 6 10 × 10 6 = 1,5

E aqui vamos ter que tomar muito cuidado, porque ambas as seções são iguais em dimensões, porém, são completamente diferentes em material, isso significa que a nossa LN não passa na interseção das seções, e para sabermos onde ela passa, vamos usar o nosso fator de transformação ali de cima. Sendo assim, a nossa LN vai ser calculada pela seguinte equação modificada com o fator de transformação:

y - = n A l a t ã o y l a t ã o + A a l u m í n i o y a l u m í n i o n A l a t ã o + A a l u m í n i o

E pra nossa seção temos que:

A l a t ã o = A a l u m i n i o = π 0,8 2 2 = 1,0   i n 2

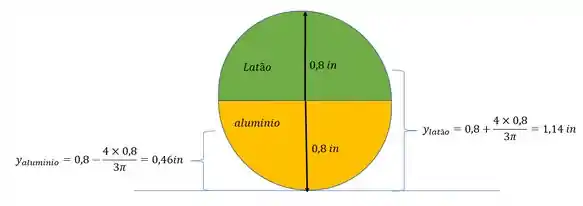
Assim temos que:

y - = 1,5 × 1,0 × 1,14 + 1,0 × 0,46 1,5 × 1,0   + 1,0 = 0,868   i n

Ou seja, a nossa LN está posicionada da seguinte maneira.

Passo 2

Para o nosso momento de inércia, a nossa equação será dada por:

I = n I - + A l a t ã o d l a t ã o 2 + ( I - + A a l u m i n i o d a l u m i n i o 2 )

Temos que:

A l a t ã o = A a l u m i n i o = π 0,8 2 2 = 1,0   i n 2

I l a t ã o = I a l u m i n i o = π 0,8 4 8 = 0,161   i n 4

Porém tem uma coisa muito importante com relação a esse exercício, o momento fletor foi aplicado na interface entre seções, e não na LN, o que isso significa? Isso significa que temos que obter o momento de inércia relativo ao ponto que ocorre a interface das seções, porém, sabendo que os centroides de ambas as seções circulares estão deslocados, ou seja, seria uma espécie de momento de inércia médio, assim a nossa fórmula é:

I - = I a l u m i n i o - A a l u m i n i o × d 0 a l u m i n i o 2

Em que:

d 0 a l u m i n i o 2 = 4 r 3 π = 4 × 0,8 3 π = 0,34   i n

Substituindo teremos que:

I - = 0,161 - 1,0 × 0,34 2 = 0,045   i n 4

E os valores de d usaremos os da imagem abaixo para nos ajudar:

I = 1,5 0,045 + 1,0 × 0,272 2 + 0,045 + 1,0 × 0,408 2 = 0,390   i n 4

Passo 3

Queremos as tensões tanto no alumínio quanto no aço, e para isso teremos que prestar atenção nos pontos que iremos determinar os valores de y tanto para o alumínio quanto no latão, e para isso, temos que ter as distancias relativas a LN.

  • y - positivo e negativo

Calculando primeiro o alumino:

M = 8 k i p ∙ i n

y - a l u m i n i o = - 0,868   i n

I = 0,390   i n 4    

σ x = - M y I

Substituindo, teremos que:

σ max ⁡ - a l u m í n i o = - 8 k i p ∙ i n - 0,868 i n 0,390   i n 4   = 17,81 k i p i n 2 = 17,81   k s i

Calculando no latão:

M = 8 k i p ∙ i n

y - l a t ã o = 0,732   i n

I = 0,390   i n 4    

n = 1,5    

σ x = - n M y I

Substituindo, teremos que:

σ max ⁡ - l a t ã o = - 1,5 8 k i p ∙ i n 0,732 i n 0,390   i n 4   = - 22,5   k i p i n 2 = - 22,5   k s i

Resposta

  1. σ max ⁡ - a l u m í n i o = 17,81   k s i

  2. σ max ⁡ - l a t ã o = - 22,5   k s i
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga composta é feita de aço A-36 (A) unido a latão vermelho C83400 (B) e tem seção transversal mostrada na figura. Se a tensão de flexão admissível para o aço for (σadm)aço = 180 MPa e para o latão
O garfo é usado como parte do conjunto do trem de pouso de um avião. Se a reação máxima da roda na extremidade do garfo for 4,5 kN, determine a tensão de flexão máxima na porção curva do garfo na seçã
Uma viga estruturada tem a seção transversal mostrada na figura. Determine (a) a localização do centro de cisalhamento O e (b) a distribuição das tensões de cisalhamento provocadas pela força cortante
Uma viga de paredes finas de espessura uniforme tem a seção transversal mostrada na figura. Determine a dimensão b para a qual o centro de cisalhamento O da seção transversal está localizado no ponto
A viga balanço AB, consistindo de um tubo de paredes finas com raio médio de 31,8m m e espessura de parede de 6,35m m . está submetida passa a uma força vertical de 2224k N . Sabendo que a linha de aç