Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 89
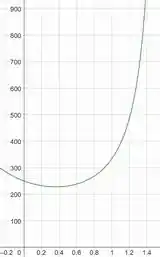
O momento constante de deve ser aplicado ao eixo de manivela. Determine a força compressiva exercida no pistão para que haja equilíbrio em função de . Represente graficamente os resultados de (eixo vertical) versus (eixo horizontal) para .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão que temos várias etapas para resolver antes de chegar na função (e o seu gráfico).
Vamos começar analisando o nosso pistão. Esboçando o seu diagrama de corpo livre, temos:
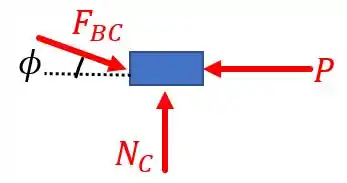
Utilizando as equações de equilíbrio, obtemos:
Mas quem é ? E quem é ? Ambos são função de . Portanto, temos que escrever cada um deles agora!
Passo 2
Das nossas duas incógnitas, vamos começar determinando .
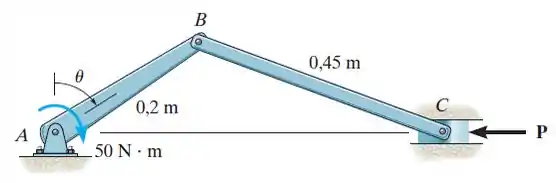
Para isto, temos que analisar a geometria do mecanismo biela-manivela. Vejamos abaixo:
Pelas relações de triângulos, obtemos:
E descobrimos a nossa primeira incógnita!
Passo 3
Agora temos que descobrir quem é . Para isto, vamos ter que analisar o braço . Então, esboçando o diagrama de equilíbrio, temos:
Fazendo o somatório de momento em torno de , vamos obter:
Substituindo a relação de que obtivemos no Passo 2, temos:
Passo 4
Agora já temos todas as informações necessárias para escrevermos . Substituindo as relações que obtivemos anteriormente, temos:
Agora só nos resta esboçarmos a função. O seu gráfico é:
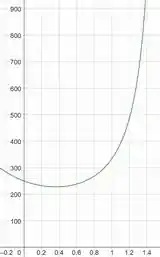
OBS: O eixo está em radiano!
Resposta
