Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 94
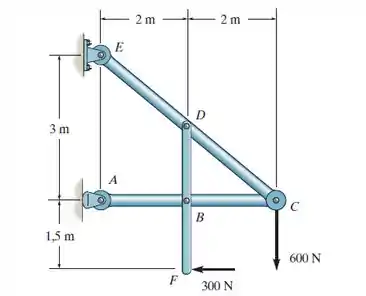
Determine as componentes horizontal e vertical da força que o pino exerce sobre o membro . A carga de 600 N é aplicada ao pino.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Temos uma estrutura contendo várias barras e queremos determinar apenas as componentes horizontal e vertical da força que o pino exerce.
Para podermos dar início a questão, precisamos determinar a reação no vínculo (e consequentemente teremos em ). Para isto, vejamos o diagrama de corpo livre abaixo:
FIGURA
Portanto, para calcularmos a reação em , vamos fazer o somatório de momento em relação ao ponto , pois assim eliminamos as incógnitas da nossa equação. Desta forma, temos:
Passo 2
Ainda não temos informação suficiente para calcularmos as reações e . Isto se decorre do fato de termos 4 incógnitas na barra (temos também e )
OBS: Se tivéssemos calculado e , também teríamos 4 incógnitas na barra ( e ).
Portanto, precisamos calcular e . Para isto, vamos esboçar o diagrama de corpo livre da barra . Portanto,
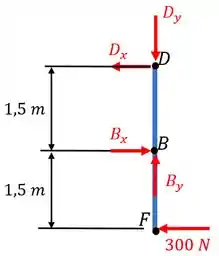
OBS: detalhe para a distância do segmento . Ele foi calculado pela relação de triângulo da geometria do problema.
Continuando, vamos calcular as reações em . Fazendo o somatório de momentos em relação a , obtemos:
E ? Como calculamos???
Bom, não temos informações suficientes aqui para calculá-lo. Mas isto não é problema! Conseguimos reduzir a barra para 3 incógnitas. Agora sim já temos como trabalhar!
Passo 3
Para finalizarmos a questão, basta trabalharmos com a barra . Fazendo o seu diagrama de corpo livre, temos:
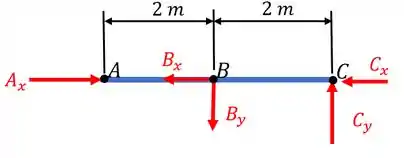
E utilizando as relações de equilíbrio, temos:
E assim finalizamos a questão!