Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 91
A máquina na figura é usada para moldar placas de metal. Ela consiste em dois mecanismos, e , operados pelo cilindro hidráulico . Os mecanismos empurram o elemento móvel para a frente, pressionando a placa para dentro da cavidade. Se a força que a placa exerce sobre a cabeça é , determine a força no cilindro hidráulico quando .
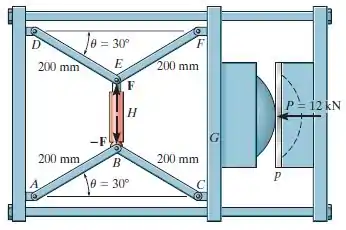
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma daquelas questões que assusta pelo desenho, mas que no final, vai sair bem fácil!
Precisamos determinar quem é a força no cilindro hidráulico quando . Para isto, sabemos que a força .
Bom, podemos resolver esta questão analisando a barra ou . Vamos escolher aqui a primeira (tanto faz na realidade).
Passo 2
Escolhida a barra, precisamos identificar quem é a força no pino em . Devido a simetria do problema, a componente na direção horizontal é exatamente a metade de . Logo, .
Já a componente vertical deve ser tal que a força resultante em deve estar na mesma direção que a barra . Para nos auxiliar, vejamos um diagrama de corpo livre abaixo:
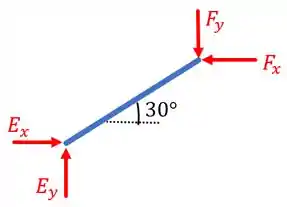
Portanto, para garantir que a força resultante em tenha a mesma direção que a barra , temos que:
E consequentemente, as reações em são:
Passo 3
Agora já podemos partir para analisar o nó . Utilizando o método dos nós, temos o seguinte diagrama de forças:
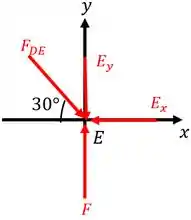
Agora, como está em equilíbrio, basta fazermos o somatório de forças em ambas as direções e igualarmos a zero. Portanto,
Resolvendo o sistema acima obtemos:
E assim finalizamos a questão!