Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 91

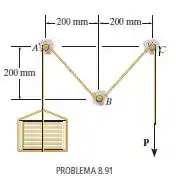
Determine a menor força P necessária para levantar a caixa de 40   k g . O coeficiente de atrito estático entre o cabo e cada pino é μ s = 0,1 .

Passo 1

Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!

O enunciado nos pede para determinar a força P mínima necessária para suspender a caixa de 40   k g , considerando que o coeficiente de atrito estático entre o cabo e os pinos é μ s = 0,1 .

Então bora lá! Para resolver esse problema, vamos analisar as polias separadamente até chegar na força P . Começando então pelo diagrama de corpo livre da polia A :

Vamos usar a seguinte relação:

T 2 = T 1 * e μ β

Onde:

T 2 = T A B

T 1 = W

W = 4 0 * 9,81 = 392,4   N

μ s = 0,1

β = 180 ° - 45 °

β = 135 ° = 3 4 π

Substituindo na equação, temos:

T A B = 392,4 * e 0,1 * 3 π 4

T A B = 496,66   N

Passo 2

Analisando agora a polia B :

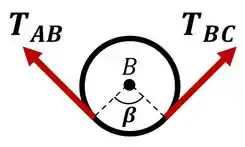
Neste caso, na equação T 2 = T 1 * e μ β temos:

T 2 = T B C

T 1 = T A B = 496,66   N

μ s = 0,1

β = 90 ° = π 2

Substituindo na equação, temos:

T B C = 496,66 * e 0,1 * π 2

T B C = 581,14   N

Passo 3

Finalmente, para a polia C :

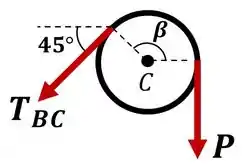
Neste caso, na equação T 2 = T 1 * e μ β temos:

T 2 = P

T 1 = T B C = 581,14   N

μ s = 0,1

β = 135 ° = 3 4 π

Substituindo na equação, temos:

P = 581,14 * e 0,1 * 3 π 4

P = 735,54   N

Resposta

P = 735,54   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

( a ) Mostre que a viga do Problema 8.34 não pode se mover se a superfície superior do carrinho é ligeiramente mais baixa que a plataforma. ( b ) Mostre que a viga pode ser movida se dois trabalhadore
A haste esbelta AB de comprimento l = 600m m é ligada a um colar em B e repousa sobre um pequeno rolete localizado a uma distância horizontal a = 80m m da barra vertical sobre a qual o colar desliza.
Duas barras idênticas de 1,5 m de comprimento conectadas por um pino em B estão colocadas entre duas paredes e uma superfície horizontal como mostrado na figur. Designando por μ s o coeficiente de atr
Dois blocos A e B de 8 kg repousam em prateleiras e são conectadas por uma barra de massa desprezível. Sabendo que a intensidade da força P aplicada em C é lentamente incrementada a partir de zero, de
Duas hastes esbeltas de peso desprezível são conectadas por um pino em C e ligadas aos blocos A e B, cada qual com peso W. Sabendo que θ = 80 ° e que o coeficiente de atrito estático entre os blocos e