Mostre que a viga do Problema 8.34 não pode se mover se a superfície superior do carrinho é ligeiramente mais baixa que a plataforma. Mostre que a viga pode ser movida se dois trabalhadores de 787,5 N estão na viga em B e determine a distância máxima para a esquerda que a viga pode ser movida.
Passo 1
Tá legal! Vamos começar esse excercício desenhando o DCL para a viga da letra :
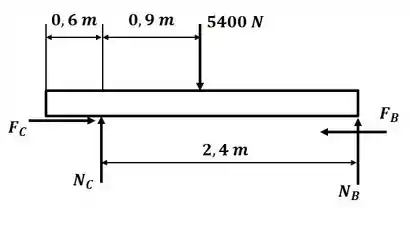
Sabemos que a força de atrito nos pontos B e C pode ser escrita como:
Passo 2
Agora vamos aplicar o somatório de momento em relação ao ponto C:
Aplicando o somatório de forças na direção :
Dessa forma, podemos calcular as forças de atrito máxima nos pontos B e C:
Como a força de atrito em C é maior do que em B, o escorregamento ocorre primeiro em B e dessa forma a viga não se move.
Passo 3
Agora vamos desenhar o diagrama de corpo livre da viga para a letra com os trabalhadores em cima:
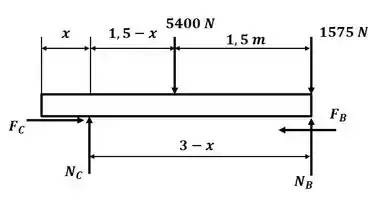
Agora vamos aplicar o somatório de momento em relação ao ponto C:
E, aplicando o somatório de forças com relação ao ponto B:
Agora, vamos fazer um teste e ver se a viga se move com os trabalhadores com a mesma distância da letra , com , substituindo o valor de nas equações para as reações:
Calculando a força de atrito máxima com essas reações, temos:
Com isso, sabemos que a viga começa a deslizar primeiro em C, então a viga se move. Agora precisamos ver o quanto a viga se move, para isso, devemos notar que a viga irá parar quando a força de atrito em C for igual a máxima força de atrito em B, ou seja:
Substituindo os valores conhecido para as duas expressões, temos:
Isolando e resolvendo para :