Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 45

Duas hastes esbeltas de peso desprezível são conectadas por um pino em C e ligadas aos blocos A e B, cada qual com peso W. Sabendo que θ = 80 ° e que o coeficiente de atrito estático entre os blocos e a superfície horizontal é 0,30, determine o maior valor de P para que o equilíbrio seja mantido.

Passo 1

Tá legal! Vamos começar esse excercício desenhando o triângulo de forças para o pino C:

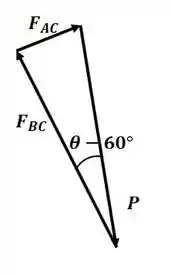
Sabemos que as forças de atrito podem ser calculadas por:

F A C = P s e n 20 ° = 0,342 P

F B C = P c o s 20 ° = 0,940 P

Agora podemos aplicar o somatório de forças na direção y para o pino C:

+ ↑ ∑ F y = 0

N A - W - F A C s e n 30 ° = 0 → N A = W - 0,342 P s e n 30 ° → N A = W + 0,171 P

Passo 2

Agora vamos analisar o diagrama de corpo livre para o bloco A:

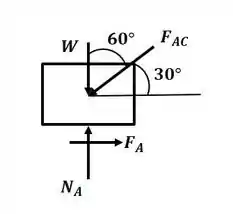
Agora aplicando o somatório de forças na direção x :

+ → ∑ F x = 0

F A - F A C cos ⁡ 30 ° = 0

F A = 0,342 P c o s 30 ° → F A = 0,296 P

Sabemos que na iminência do movimento em A, temos a força de atrito sendo:

F A = μ s N A → N A = F A μ s

Substituindo os valores encontrados para N A e F A :

W + 0,171 P = 0,296 P 0,3 → P = 1,225 W

Agora aplicando o somatório de forças na direção y :

+ ↑ ∑ F y = 0

N B - W - F B C cos ⁡ 30 ° = 0 → N B = W + 0,940 P c o s   30 °

N B = W + 0,814 P

E, agora, aplicando o somatório de forças na direção x :

+ → ∑ F x = 0

F B C s e n 30 ° - F B = 0 → F B = 0,940 P s e n 30 ° → F B = 0,47 P

Passo 3

Agora iremos analisar o diagrama de corpo livre para o bloco B:

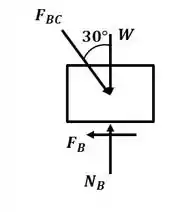
A força de atrito pode ser escrita como:

F B = μ s N B → N B = F B 0,3

Substituindo os valores encontrados para N B e F B :

W + 0,814 P = 0,47 P 0,3 → P = 1,33 W

Dessa forma, para manter o equilíbrio, o máximo valor de P deve ser o menor entre os dois valores encontrados, ou seja:

P = 1,225 W

Resposta

P = 1,225 W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada um dos cilindros tem uma massa de 50k g . Se os coeficientes de atrito estático nos pontos de contato são μ A = 0,5 , μ B = 0,5 , μ C = 0,5 e μ D = 0,6 , determie o menor momento de binário M nec
Se θ = 15 ° , determine o menor coeficiente de atrito estático entre os colares A e B e a barra necessário para que o sistema permaneça em equilibrio, independente do peso do cilindro D . As ligações
Determine a menor força P que causará a iminência de movimento. A caixa e a roda têm uma massa de 50k g e 25k g , respectivamente. O coeficiente de atrito estático entre a caixa e o piso é μ s = 0 , 5
Os blocos A , B e C possuem pesos de 250N , 125N e 75N , respectivamente. Determine a menor força horizontal P que causará iminência de movimento. O coeficiente de atrito estático entre A e B é μ s =
Determine a menor força P que causará a iminência de movimento. A caixa e a roda têm uma massa de 50k g e 25k g , respectivamente. O coeficiente de atrito estático entre a caixa e o piso é μ s = 0,2 ,