Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 42

Dois blocos A e B de 8 kg repousam em prateleiras e são conectadas por uma barra de massa desprezível. Sabendo que a intensidade da força P aplicada em C é lentamente incrementada a partir de zero, determine o valor de P para qual movimento ocorre, e qual é o movimento, quando o coeficiente de atrito estático entre todas as superfícies é a μ s = 0,40 ,   b μ s = 0,50 .

Passo 1

Tá legal! Vamos começar esse excercício desenhando o diagrama de corpo livre para o sistema:

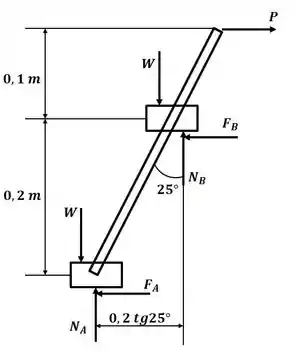
Sabemos que as forças de atrito podem ser calculadas por:

F B = μ s N B

F A = μ s N A

Agora podemos aplicar o somatório de forças na direção y :

+ ↑ ∑ F y = 0

N A + N B - 2 W = 0 → N A + N B = 157   N

Agora aplicando o somatório de forças na direção x :

+ → ∑ F x = 0

P - F A - F B = 0 → P = μ s N A + μ s N B

P = μ s N A + N B

Substituindo o valor encontrado para N A + N B e o valor de μ s para a letra ( a ) , temos:

P = 0,4 157 → P = 62,8   N

Passo 2

Agora, aplicando o somatório de momento em relação ao ponto B:

+ ↻ ∑ M B = 0

P 0,1 - N A 0,2 t g 25 ° + W 0,2 t g 25 ° + 0,4 N A 0,2 = 0

62,8 0,1 - N A 0,2 t g 25 ° + 78,5 0,2 t g 25 ° + 0,4 N A 0,2 = 0 → N A = 6   N

Temos reação em A, o que quer dizer que o sistema se desloca.

Passo 3

Agora, analisando para o caso da letra ( b ) :

P = μ s N A + N B = 0,5 157 → P = 78,5   N

Agora, aplicando o somatório de momento em relação ao ponto B:

+ ↻ ∑ M B = 0

P 0,1 + N A 0,2 t g 25 ° - W 0,2 t g 25 ° + 0,5 N A 0,2 = 0

78,5 0,1 + N A 0,2 t g 25 ° - 78,5 0,2 t g 25 ° + 0,5 N A 0,2 = 0 → N A = - 2,73   N

Como a força de reação nesse caso deu negativa, na verdade o sistema rotaciona ao redor de B. Dessa forma, aplicando o somatório de momento em relação ao ponto B:

+ ↻ ∑ M B = 0

P 0,1 - W 0,2 t g 25 ° = 0 → P = 73,2   N

Resposta

P = 62,8   N

P = 73,2   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se cada caixa pesa 75k g , determine a menor força horizontal P que o homem precisa exercer na caixa de cima a fim de causar movimento. O coeficiente de atrito estático entre as caixas é μ s = 0 , 6 5
Se a garota com 35k g estiver na posição d = 1,2m , determine o coeficiente mínimo de atrito estático μ s nos pontos de contato A e B de modo que a tábua não deslize. Despreze o peso da tábua.
Se o coeficiente de atrito estático nos pontos de contato A e B é μ s = 0,4 , determine a distância mínima d onde uma garota de 35k g pode permanecer sobre a tábua sem que a tábua deslize. Despreze o
Se os coeficientes de atrito estático nos pontos de contato A e B são μ s = 0 , 3 e μ s ' = 0 , 4 , respectivamente, determine a menor força P que fará com que o carrretel de 150k g tenha iminência de
Se o coeficiente de atrito estático entre os colares A e B e a barra é μ s = 0,6 , determine o ângulo máximo θ para o sistema permanecer em equilíbrio, independente do peso do cilindro D . As ligações