Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 93
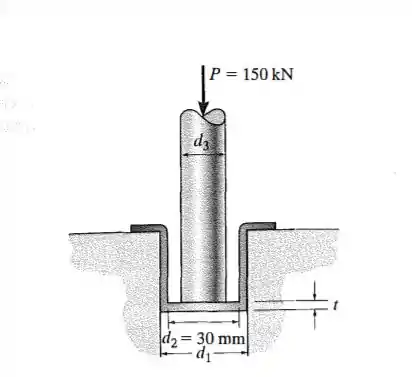
Determine as menores dimensões do eixo circular e da tampa circular se a carga que devem suportar é . A tensão de tração, a tensão de apoio e a tensão de cisalhamento admissíveis são e .
Passo 1
Fala!
Como queremos dimensionar componentes que se relacionam com a área e nos foi dada as tensões médias admissível, devemos nos lembrar como se calcula essa tensão média que é dada por
Mas repara que a gente precisa dimensionar os diâmetros do eixo e da tampa. O eixo está sofrendo com tensão normal.
A tampa sofre tensão normal e de cisalhamento.
Tendo isso em mente, vamos analisar aí essas 3 situações!
Obs: a última tensão que ele deu de na verdade deveria estar escrita como , porque é de cisalhamento.
Passo 2
Vamos olhar para a tampa. Esse eixo com força para baixo faz com que uma tensão de tração seja gerada nas paredes da tampa, para que a base da tampa não caia, assim:
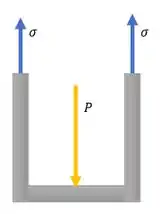
Quem aguenta a tensão normal é a parede da tampa, de diâmetro interno e externo . Para esse material, a tensão de tração dada é . Temos
Passo 3
Agora vamos olhar a tensão normal no eixo. Toda a sua área suporta a força. Para o caso de tensão de apoio a geometria é de um círculo assim teremos
Passo 4
Agora vamos olhar a situação de cisalhamento na tampa. Sobre ela temos o eixo.
O nosso eixo é um tubo. Então quando a gente aplica essa carganele, ela é transmitida para a tampa assim:
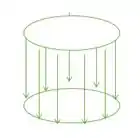
De forma que a área da tampa que é paralela a esse carregamento (a área que sofre cisalhamento) na real é área lateral de um cilindro contido na tampa.
E quem é esse cilindro? O diâmetro dele é o diâmetro do eixo. E a altura dele é a espessura da tampa. Assim essa área onde ocorre cisalhamento é:
Por fim, para a tensão normal admissível vamos ter