Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 87

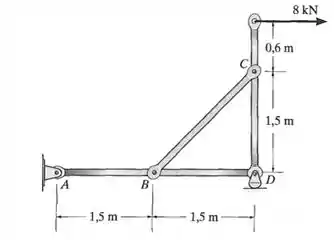
A estrutura está sujeita a carga de 8   k N . Determine o diâmetro exigido para os pinos em A e B se a tensão de cisalhamento admissível para o material for τ a d m =   42   M P a . O pino A está sujeito a cisalhamento duplo, ao passo que o pino B está sujeito a cisalhamento simples.

Passo 1

Caraaa, então precisamos achar as forças aplicadas nesses pinos através das barras. Vamos começar achando as reações de apoio.

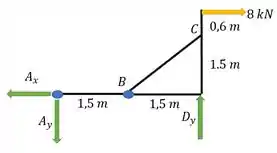
Pelas equações de equilíbrio, temos:

∑ M d = 0

Adotando o sentido anti-horário como positivo vamos ter

3 A y - 8 ⋅ 2.1 = 0

A y = 5,6   k N

∑ F y = 0

A y = D y = 5,6   k N

∑ F x = 0

A x = 8   k N

Passo 2

Temos que o esforço no pino A é a resultante da força em A , então a gente pode usar a fórmula de tensão média nele. E aí no lugar da tensão média colocamos a tensão máxima permitida, com isso achamos o diâmetro.

Lembrando que a tensão de cisalhamento é dada por

τ m e d = V A → A = V τ m e d

π 4 ⋅ d 2 = V τ m e d

d 2 = 4 π ⋅ V τ m e d

d = 4 π ⋅ V τ m e d

Onde V = F A 2 devido ao cisalhamento duplo nesse pino. E a força resultante em A é:

F A = A x 2 + A y 2 = 9,76   k N

d = 4 π ⋅ F A 2 τ m á x

Dessa forma vamos obter

d a = 12,166 m m

Passo 3

A força resultante sobre ele é a força saindo do segmento B C . Vamos achar ela, substituindo esse segmento pela força. E calculando o somatório de momentos em relação a D .

F B C ⋅ s i n θ ⋅ 1,5 m = 5,6 k N ⋅ 3 m

Como θ = 45 ° conseguimos encontrar F B C facilmente

F B C = 5,6 * 3 1,5 ⋅ s i n 45 ° ≈ 15,839 k N

Para o pino B teremos

d = 4 π ⋅ V τ m e d

Onde V = F B C , assim

d b = 4 π ⋅ F B C τ m e d ≈ 21,913 m m

Resposta

d a = 12,166 m m   e   d b = 21,913 m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o estado de tensões dado, determinar as tensões, normal e de cisalhamento, depois que o elemento mostrado tenha sofrido uma rotação de:(b) 15 no sentido horário
Uma força de 19,5kN é aplicada no ponto D da barra de ferro fundido mostrada. Saendo-se que a barra tem um diâmetro de 60mm, determinar as tensões principais e a máxima tensão de cisalhamento no:(a) p
Para o estado de tensões dado, determinar as tensões, normal e de cisalhamento, depois que o elemento mostrado tenha sofrido uma rotação de:(a) 40 no sentido anti-horário
Uma força de 19,5kN é aplicada no ponto D da barra de ferro fundido mostrada. Saendo-se que a barra tem um diâmetro de 60mm, determinar as tensões principais e a máxima tensão de cisalhamento no:(a) p
Duas forças são aplicadas como mostrado na barra AB, que é soldada ao cilindro DE, de diâmetro 50mm. Considerando que todas as tensões permanecem abaixo do limite de proporcionalidade, determinar as t