Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 78
Determine o módulo que deve ser aplicado em , para manter o suporte em equilíbrio estático na posição mostrada. Calcule também o módulo da reação do pino em .
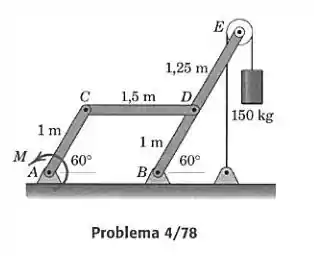
Passo 1
Pra obter os dados que o problema pede, precisamos aplicar as equações de equilíbrio na barra , e pra isso precisamos da força da barra . Por outro lado encontramos a força aplicando equações de equilíbrio para a barra . Vamos então representar e em diagramas de corpo livre. Representamos também o diagrama para a polia, pois envolve a força em para a barra .
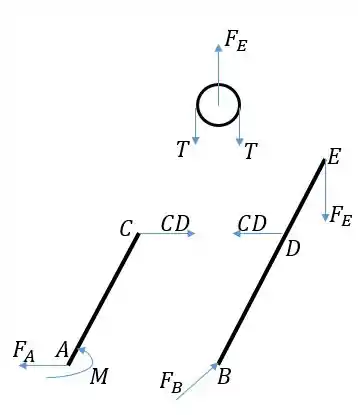
Passo 2
Primeiro usamos o diagrama da polia pra calcular a força :
Agora, fazendo para a barra o momento em torno de , encontramos :
Substituindo pelo valor de encontrado anteriormente:
Passo 3
Agora para a barra , fazendo a soma dos momentos em torno de ser zero encontramos :
Pelo equilíbrio horizontal da barra: