Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 73

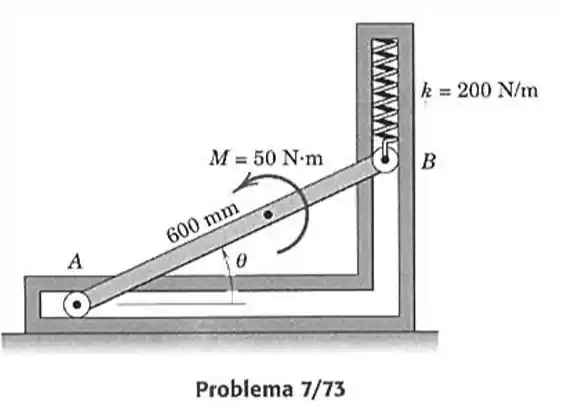
73- Os roletes nas extremidades da barra uniforme A B , de 10   k g , se movem livremente nas guias horizontal e vertical, como mostrado. Determine a posição de equilíbrio θ para a barra sob a ação de um momento M = 50   N m e da mola com rigidez k = 200   N / m . A mola não está comprimida quando θ = 0 .

Passo 1

Primeiramente vamos analisar as energias estáticas que estão presentes no sistema e depois dessa análise podemos fazer com que:

δ U = δ V

Uma vez que temos o momento no meio da barra que faz com que haja um trabalho externo.

Desenhando os eixos de energia potencial nula e encontrar essas energias potenciais.

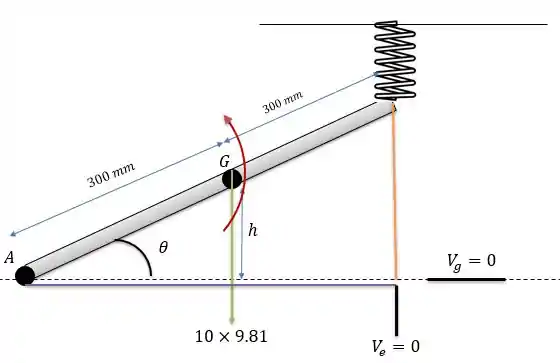
Para encontrar a energia potencial gravitacional do sistema basta sabermos que o centro de massa da barra encontra-se no meio geométrico da barra e rebater sua posição na vertical, na figura conseguimos ver que é o tamanho h , que será dado por:

sin ⁡ θ = h 300   m m → h = 0.3 sin ⁡ θ

Logo a energia potencial gravitacional do sistema será:

V g = m g h = 10 × 9.81 × 0.3 sin ⁡ θ = 29.43 sin ⁡ θ

Agora para encontrar a energia potencial elástica, precisamos ver que quando θ = 0 a mola não está esticada e ocupa todo o espaço preenchida pela reta laranja, logo quando percorrido o ângulo θ a compressão da mola será todo o tamanho da reta laranja que será:

sin ⁡ θ = r e t a   l a r a n j a 600 m m → r e t a   l a r a n j a = 0.6 sin ⁡ θ

Logo a energia potencial elástica será de( com K = 200   N / m )

V e = 1 2 × 200 ( 0.6 sin ⁡ θ ) 2 = 36 sin 2 ⁡ θ

Logo a energia potencial total do sistema será de:

V = 36 sin 2 ⁡ θ + 29.43 sin ⁡ θ

Passo 2

Como o momento exercido no meio da barra faz um trabalho efetivo nós devemos considerar que para haver equilíbrio no sistema a devida condição tem que ser atendida:

d U = d V

Onde d U que é a influência do momento será dada por:

d U = 50 d θ

Logo :

50 d θ = 36 × 2 × sin ⁡ θ cos ⁡ θ d θ + 29.43 cos ⁡ θ   d θ

Onde se cortarmos d θ e aplicarmos a solução trigonométrica sin ⁡ 2 θ = 2 × sin ⁡ θ cos ⁡ θ   nós vamos ter:

50 = 36 sin ⁡ 2 θ + 29.43 cos ⁡ θ

Passo 3

Se plotarmos o gráfico de 36 sin ⁡ 2 θ + 29.43 cos ⁡ θ - 50   e vermos onde essa função será zero nós encontramos:

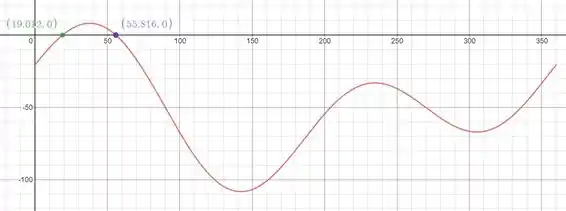
Vemos como respostas θ = 19.012 ° e θ = 55.816 ° como posições de equilíbrio. Agora para a estabilidade, vamos fazer a derivada segunda da energia que nos daria.

d V 2 d 2 θ = 72 cos ⁡ 2 θ - 29.43 sin ⁡ θ

Plotando esse gráfico temos a seguinte curva azul.

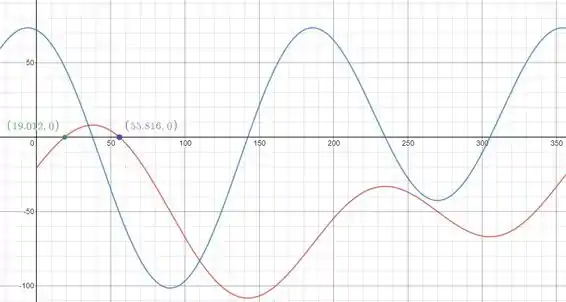
Que pela curva ser positiva em θ = 19.012 ° temos que essa posição é uma posição estável e em θ = 55.816 ° está curva é negativa, nos indicando uma posição instável.

Resposta

θ = 19.012 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O ‘pantógrafo de Nuremberg’ está sujeito a uma força horizontal P=600 N. Determine o ângulo θ para o equilíbrio. A mola tem uma rigidez k = 15 kN/m e está livre quando θ=15º
O mecanismo conectado por pinos é restrito em A por um pino e em B por um rolete. P = 50 N, determine o ângulo θ para o equilíbrio. A mola está livre quando θ = 45 º º. Despreze o peso de ambos
Se uma força P = 25 N é aplicada à alça do mecanismo, determine a força que o parafuso exerce sobre a rolha da garrafa. O parafuso está conectado ao pino em A e passa pelo colar que está conectado à b
Determine a força desenvolvida na mola exigida para manter a barra uniforme AB de 50 N ( ≈ 5 kg) em equilíbroo quando θ = 35º
O ‘pantógrafo de Nuremberg’ está sujeito a uma força horizontal P = 600 N. Determine a rigidez k para o equilíbrio quando θ=60º . A mola está livre quando θ=15º.