Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.9 - Ex. 2iii

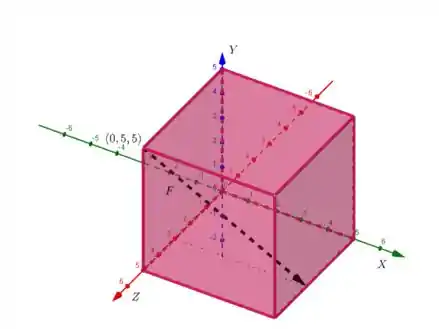
Determine os momentos das forças representadas na próxima figura, em relação às origens dos sistemas cartesianos indicados

Passo 1

Nessa questão, podemos identificar que a força tem origem no ponto ( 0,5 , 5 ) e suas componentes são F → = ( 5   , - 5 , - 2 ) . Os sinais negativos aparecem porque F Y   e F Z apontam nas direções negativas de y e z , respectivamente. Logo, o momento da força é

M X = 5 ⋅ ( - 2 ) - 5 ⋅ ( - 5 ) = 15

M Y = 5 ⋅ 5 - 0 ⋅ ( - 2 ) = 25

M Z = 0 ⋅ ( - 5 ) - 5 ⋅ 5 = - 25

⇒ M → = 15 i ^ + 25 j ^ - 25 k ^

Resposta

M → = 15 i ^ + 25 j ^ - 25 k ^

Exercícios de Livros Relacionados

A força horizontal de 20N atua sobre o cabo da chave de soquete. Determine o momento dessa força em relação ao ponto O. Especifique os ângulos diretores coordenados α ,β ,γ do eixo do momento.
A força horizontal de 20N atua sobre o cabo da chave de soquete. Qual é o momento dessa força em relação ao ponto B? Especifique os ângulos diretores coordenados α , β , γ do eixo do momento.
A força F = {600i + 300j - 600k} N atua na extremidade da viga. Determine o momento dessa força em relação ao ponto A.
A força F age perpendicularmente ao plano inclinado. Determine o momento produzido por F em relação ao ponto B. Expresse o resultado como um vetor cartesiano.
A força F = 30 N atua sobre o suporte conforme mostrado na figura. Determine o momento da força em relação ao eixo a–a do encanamento se α=60 º ,β =60 ºeγ=45 º º º º. Além disso, determine os ângulos