Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas Fundamentais - Ex. 11
Determine o momento da força em relação ao ponto . Expresse o resultado como um vetor cartesiano.
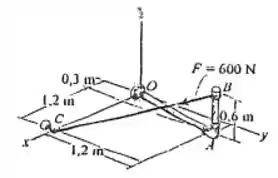
Passo 1
Para determinar o momento da força, é necessário determinar o vetor unitário , que dará a direção da nossa força, o vetor posição ou que nos dá a distância do braço da força até o ponto onde avaliamos o momento e a força como um vetor cartesiano ().
Assim, será possível determinar o momento gerado a partir do produto vetorial:
Podemos fazer tanto com o vetor posição quanto com o vetor posição , afinal, ambos nos darão a distância do braço da força até o eixo do momento.
Bom galera, primeiro passo aqui, vai ser encontrar a nossa força , que vai ser dada por:
Passo 2
Logo, o vetor unitário é dado por:
Onde esses termos aí, indicam as componentes da distância entre os pontos B e C...
Olhando a nossa figura, podemos indicar que:
Show de bolê, agora a gente substitui:
Agora, a nossa força como vetor cartesiano será:
Para continuar, precisamos dos vetores posição...
Dando uma olhada na figura, também podemos encontrar as componentes dos vetores posição, e assim escreve-los vetorialmente:
E:
Agora, vamos para o produto vetorial!
Passo 3
Por fim, temos duas formas para calcular o momento, você pode escolher a sua!
1)
O momento será:
E, aplicando o determinante para solucionar esse produto vetorial, teremos:
Ou seja:
2)
O momento também pode ser dado por:
E o seu determinante será dado por:
Portanto:
Resposta
O momento gerado pela força em relação ao ponto é: