Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 27
27- No Problema determine a distância perpendicular do ponto até o cabo .
Passo 1
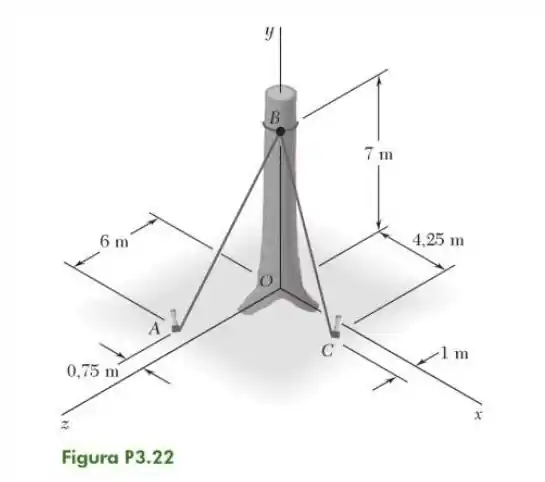
Se dermos uma olhada rapidão no exercício 22 vemos que a força no cabo vale . Agora vamos desenhar uma reta com distância que sai de e que encontra a corda em ângulo perpendicular de forma que teremos :
Essa força é a força no cabo que independe do seu sentido e da direção na corda ela será o valor de força na corda igual a:
Até existe uma maneira em geometria analítica para fazer isso, mas po estamos num livro de física, vamos usar a física a nosso favor aqui.
Passo 2
Já o momento será o módulo do momento em e para isso precisamos da vetorização de no cabo que será:
Dessa forma o momento vetorial será:
Então o momento vetorizado:
O que nos dá um valor absoluto de módulo igual a:
Passo 3
Logo a distância será: