Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 70
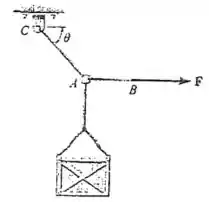
A caixa de 250 kg é suspensa usando as cordas AB e AC. Cada corda pode suportar uma tração máxima de 12,5 kN antes de se romper. Se AB permanece na horizontal, determine o menor ângulo no qual a caixa pode ser suspensa.
Passo 1
Fala, querido! Ele quer aquele ângulo para que a força nas cordas não ultrapasse .
Para encontrar o ângulo, que deve ser feita a análise e o equilíbrio de forças no plano bidimensional, ou seja, em x e y.
Assim, é possível determinar o ângulo já que haverá uma força em função dele nas equações de equilíbrio.
Além disso, o peso da caixa é dado por .
Vamos fazer um DCL do ponto para depois aplicarmos as equações de equilíbrio nele
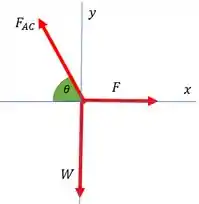
Passo 2
Logo, o equilíbrio requer que:
Aqui vamos precisar decompor as forças nos eixos coordenados. Adotando como sentido positivo os sentidos para a direita (eixo x) e para cima (eixo y):
Passo 3
Vamos refletir. Ele disse que a maior tensão nas cordas não pode ultrapassar . Aí para substituir esse valor nas nossas equações, precisamos ver quem é a maior tensão, ou .
A gente pode ver isso olhando :
Agora a gente vai lembrar de algo beeem antigo. O cosseno está sempre entre e . Isso quer dize que quando a gente multiplica cosseno por , o resultado vai ser um valor menor que . Cara, a nossa equação diz que é esse resultado. Então:
Logo, é a maior tensão e na situação limite, temos
Agora, como a força não foi dada, é possível analisar a equação (2) e achar nosso ângulo.
Então, analisando a equação em questão, tem-se: