Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 23
23- Uma barra de tem um ponta fixada em . Um cabo de aço é esticado da ponta livre da barra ao ponto localizado na parede vertical. Se a tensão no cabo é , determine o binário que a força exerce sobre através do cabo em .
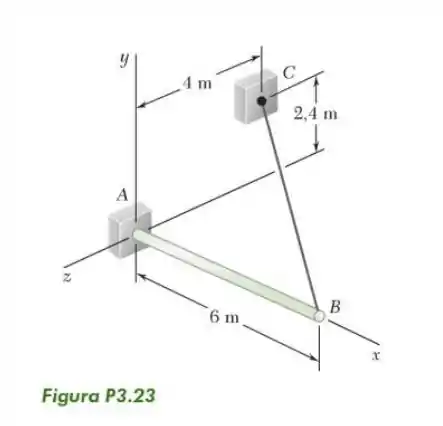
Passo 1
Vamos desenhar o diagrama de forças na barra .
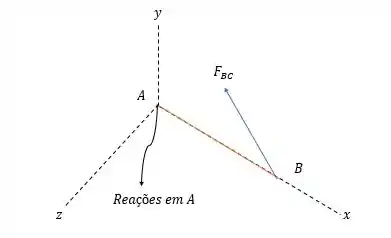
Por ser um apoio tipo engaste nós teremos reações em forças e em momentos em que suportam toda a carga e que terá o mesmo módulo das forças e dos momentos na barra (já que cortamos a barra do resto do sistema).
A força valerá:
Agora a distância de para será simplesmente:
Passo 2
Dessa forma o momento binário será:
Pois se o momento em causado pela corda em em x for no sentido horário, enão deverá surgir uma no anti-horário em para que o corpo não gire, por isso o sinal.
Isso nos dará: