Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 86

Determine o momento de plastificação M p da viga de aço da seção transversal mostrada na figura, considerando que o aço é elastoplástico com uma tensão de escoamento de 248   M p a .

Passo 1

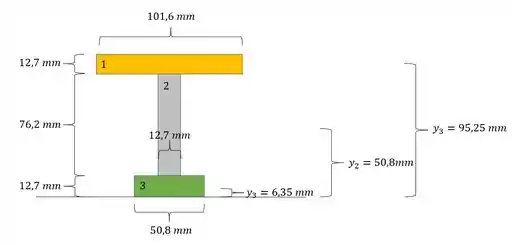
Antes de determinarmos o momento plástico, precisamos determinar a LN, e para isso temos a seguinte equação:

y - = A 1 y 1 + A 2 y 2 + A 3 y 3 A 1 + A 2 + A 3

Assim temos que:

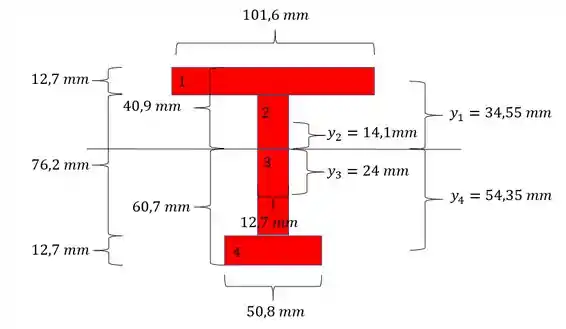
y - = 12,7 × 101,6 × 95,25 + 12,7 × 76,2 × 50,8 + 12,7 × 50,8 × 6,35 12,7 × 101,6 + 12,7 × 76,2 + 12,7 × 50,8

y - = 60,7   m m

Para determinação no momento plástico, consideramos a seção inteiramente plastificada, ou seja, podemos definir a seguinte seção:

E sabemos que a região plástica, nada mais é que a região onde a tensão de escoamento é constante, ou seja, podemos fazer o seguinte diagrama:

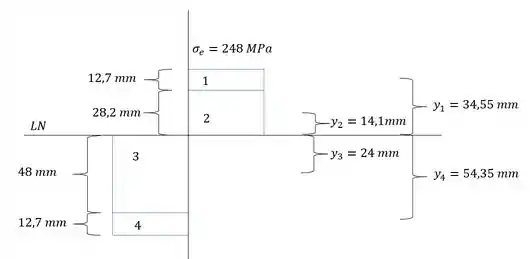
Sabemos que a força é determinada por:

F 1 = A 1 σ E = 12,7 m m × 101,6 m m × 248 N m m 2 = 320000   N

F 2 = A 2 σ E = 12,7 m m × 28,2 m m × 248 N m m 2 = 88818,72   N

F 3 = A 3 σ E = 12,7 m m × 48 m m × 248 N m m 2 = 151180,8   N  

F 4 = A 4 σ E = 12,7 m m × 50,8 m m × 248 N m m 2 = 160000 N

M P = F 1 y 1 + F 2 y 2 + F 3 y 3 + F 4 y 4 + F 5 y 5

M P = 320000   N × 34,55 m m + 88818,72   N × 14,1 m m + 151180,8   [ N ] × 24 [ m m ] + 160000 [ N ] × 54,35 [ m m ]

M P = 24632683   N m m = 24,6   k N m

Resposta

M P = 24,6   k N m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o módulo da seção plástica e o fator de forma da seção transversal.
A viga é feita de um material elástico perfeitamente plástico. Determine o momento elástico máximo e o momento plástico que podem ser aplicados à seção transversal. Considere a = 50 mm e σe = 250 MPa.
A viga é feita de um material elástico perfeitamente plástico para o qual σe = 250 MPa. Determine a tensão residual nas partes superior e inferior da viga após a aplicação e posterior remoção do momen
Determine o módulo da seção plástica e o fator de forma da seção transversal da viga.
A haste tem seção transversal circular. Se for feita de um material elástico plástico, determine o momento elástico máximo e o momento plástico que podem ser aplicados à seção transversal. Considere r