Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 164

Determine o módulo da seção plástica e o fator de forma da seção transversal.

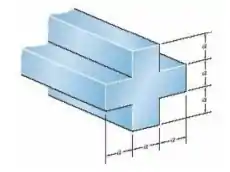
Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que tem essa viga tem um formato de cruz, com seus lados medindo a. Então, precisamos encontrar o módulo da seção plástica e o fator de seção transversal. Partiu??

Passo 2

Ok, nós vamos começar pensando na barra. Ela é redonda e sem nenhum tipo de anomalia no meio, certo?? Então, nossa linha elástica será bem no meio, e as nossas forças de tração (Tn) e contração (Cn) serão iguais aos pares, ou seja:

T 1 = C 1 (mais na borda) T 2 = C 2 (mais para o centro)

Sabendo disso, vamos calcular nosso T1 (ou C1, como preferir) inicial.

C 1 = T 1 = ( 0,5   h -   y e )   .   σ e   .   b   C 1 = a ² . σ e  

Agora, vamos calcular nosso T2 (ou C2, tira aí no par ou ímpar).

C 2 = T 2 = 0,5   y e   .   σ e   .   b   C 2 = 1,5   a ² . σ e

Passo 3

Feito isso, precisamos descobrir nossos momentos plástico e elástico e o momento de inércia do material.

I =   a ( 3 a ) 12 + 2 a ( a ) ³ 12 = 2,41667 a 4

M p =   2 a C 1 + 0,25 a C 2 = 2,57   a ³   σ e

σ e =   M e . c I       ∴     M e =   π . a ³ 4   σ e = 1,6111   a ³ σ e

Finalmente, podemos botar nas fórmulas do módulo da seção plástica e do fator da seção transversal.

k =   M p M e = 1,7 1 Z =   M p σ e = 2,75 a ³

Resposta

k =   1,7 1 Z =   2,75 a ³

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A tensão de flexão admissível para a barra é σadm = 175 MPa. Determine o momento máximo M que pode ser aplicado à barra..
A barra prismática AB é feita de uma liga de bronze para a qual a curva tensão-deformação especifica em tração é mostrada na figura. Considerando que a curva de σ em função de ϵ é a mesma em compressã
Determine o momento plástico M P , de uma viga de aço com a seção transversal mostrada, admitindo que o aço é elastoplástico com resistência ao escoamento de 240M P a .
Um pequeno segmento de perfil laminado com seção W 8 × 31 suporta uma placa rígida na qual duas cargas P eQ , são aplicadas conforme mostrado. As deformações nos dois pontos A e B na linha de centro d
Com o objetivo de incrementar a resistência à corrosão, um revestimento de alumínio com espessura de 2m m foi aplicado à barra de aço mostrada. O módulo de elasticidade é de 200G P a para o aço e de 7