Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.9 - Ex. 12

A partir do próximo capítulo serão consideradas estruturas constituídas de barras. E a próxima figura representa duas ligações de extremidades de barras metálicas em cantoneira, cujos eixos geométricos estão indicados em traço-ponto (em um sistema estrutural idealizado como treliça plana que será estudado no próximo capítulo). Calcule as forças F → 1 e F → 2 indicadas para que essas ligações estejam em equilíbrio

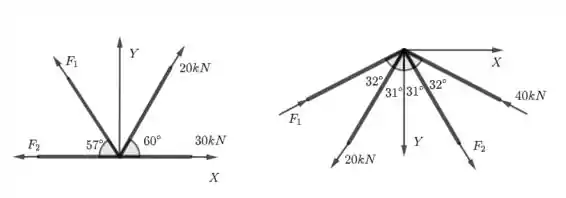
Passo 1

Vamos começar identificando as forças atuando no sistema.

  • A força de 30   k N aponta para a direita, então F → 30 = 30   k N   i ^ ;
  • A força de 20 kN está faz   60   ° com o eixo x . Então

    • F → 20 =   ( 20   k N   c o s   60   °   ) i ^ + (   20   k N   s e n   60   ° )   j ^ = ( 20   k N   ⋅ 0,5 ) i ^ + (   20   k N   0,866 )   j ^

    F → 20 =   10   k N   i ^ + 17,3   k N   j ^

  • A força F → 1 faz 57 ° e aponta para o lado negativo de x . Então,

    • F → 1 =   - F 1   c o s   57 °   i ^ + F 1   s e n   57 °   j ^   = - ( F 1 ⋅   0,545 )     i ^ + ( F 1   ⋅ 0,839 )   j ^  

  • A força F → 2 só tem componentes em x e aponta para a esquerda. Logo, F → 2 = - F 2   i ^ .

Passo 2

Com todas as forças identificadas, podemos utilizar utilizar as equações de equilíbrio:

∑ F X = 30   k N   + 10   k N   - F 1 X - F 2 = 0   ⇒   F 1 X + F 2 = 40   k N  

∑ F Y = 17,3   k N + F 1 Y = 0   ⇒ F 1 Y = - 17,3   k N  

O sinal negativo indica que na verdade a componente em y de F → 1 aponta para baixo. Em módulo, temos

| F 1 Y | = 0,839   F 1     ⇒   F 1 = 17,3   k N 0,839 ≈ 20,6   k N

Utilizando o valor de F 1 , obtemos F 1 X = 0,545 ⋅ 20,6   k N = 11,2   k N . Substituindo esse resultado na primeira equação, obtemos

F 2 = 40   k N - F 1 X = 40   k N   - 11,2   k N = 28 , 8   k N  

Assim, temos

F → 1 =   - 11,2   k N     i ^ - 17,3   j ^  

F → 2 = - 28,8   k N

Passo 3

Na segunda figura, os ângulos da parte esquerda são iguais aos da direita. Nesse caso, temos as seguintes forças:

  • A força 40   k N faz um ângulo de 31   ° + 32 ° = 63 ° com o eixo y . Logo, o ângulo com o eixo x é 90 ° - 63 ° = 27 ° . Além disso, F → 40 aponta nos sentidos negativos de x e y . Logo, temos

F → 40 = - ( 40   k N   c o s   27 ° )   i ^ - ( 40   k N   s e n   27 ° ) j ^ = - 0,891 ⋅ 40 k N   i ^ - 0,454 ⋅ 40   k N j ^  

F → 40 = - 35,6   k N   i ^ - 18,1   k N   j ^

  • A força F → 2 faz um ângulo de 31   ° com o eixo y , ou seja, um ângulo de 90 ° - 31 ° = 59 ° com o eixo x . Assim,

F → 2 = F 2 x   i ^ + F 2 Y   j ^ = F 2   c o s   59 °   i ^ + F 2   s e n   59 °   j ^ = 0,515   F 2   i ^ + 0,857   F 2     j ^

  • A força 20   k N forma um ângulo 59 ° mas aponta na direção negativa de x . Assim

F → 20 = - ( 20   k N   c o s   59 ° )   i ^ + ( 20   k N   s e n   59 ° ) j ^ = - 0,515 ⋅ 20 k N   i ^ + 0,857 ⋅ 20   k N j ^  

F → 20 = - 10,3   k N   i ^ + 17,1   k N   j ^

  • A força F → 1 aponta nos sentidos positivo de x e negativo de y e forma um ângulo 27 ° com o eixo x . Assim,

F → 1 = F 1 x   i ^ + F 1 Y   j ^ = F 1   c o s   27 °   i ^ - F 1   s e n   27 °   j ^ = 0,891   F 1   i ^ - 0,454   F 1     j ^

Passo 4

Substituindo as componentes das forças nas equações de equilíbrio, obtemos

∑ F X = - 35,6   k N   + 0,515   F 2 - 10,3   k N + 0,891   F 1 = - 45,9 k N   + 0,515   F 2 + 0,891   F 1 = 0  

⇒ 0,515   F 2 + 0,891   F 1 = 45,9 k N

∑ F Y = - 18,1   k N + 0,857   F 2 + 17,1   k N   - 0,454   F 1 = - 1,0   k N   + 0 , 857   F 2   - 0,454   F 1 = 0

⇒ 0,857   F 2   - 0,454   F 1 = 1,0     k N

Temos agora um sistema de equações:

0,515   F 2 + 0,891   F 1 = 45,9 k N

0,857   F 2   - 0,454   F 1 = 1,0     k N

Vamos utilizar a segunda equação para escrever F 2   em termos de F 1   :

0,857   F 2   = 0,454   F 1 + 1,0     k N   ⇒   F 2   =   0,454   F 1 + 1,0     k N 0,857 ≈ 0,530   F 1 + 1,177   k N

Agora substituímos essa relação na primeira equação para obter F 1 :

0,515   F 2 + 0,891   F 1 = 0,515   ( 0,530   F 1 + 1,177   k N ) + 0,891   F 1

= 0,273   F 1 + 0,606 k N + 0,891   F 1 ≈ 1,16   4 F 1 + 0,606 k N = 45,9 k N  

⇒ 1,164   F 1 = 45,9   k N - 0,606   k N = 45,29   ⇒ F 1 = 45,29   k N 1,164 ≈ 38,9   k N  

Agora que temos F 1 , podemos obter F 2 :

F 2   =   0,53   F 1 + 1,17   k N = 0,53 ⋅ 38,9   k N + 1,17   7 k N = 20,62   k N + 1,177   k N   ≈ 21,8   k N

Ok, agora que temos os módulos de F → 1 e F → 2 , podemos obter suas componentes:

F → 1 = 0,891   F 1   i ^ - 0,454   F 1     j ^ = ( 0,891 ⋅ 38,9   k N )   i ^ - ( 0,454 ⋅ 38,9   k N )     j ^

≈ 34,7   k N   i ^ - 17,7   k N     j ^

F → 2 = ( 0,515   ⋅ 21,8   k N )   i ^ + ( 0,857 ⋅ 21,8   k N )     j ^ = 11,2   k N     i ^ + 18,7   k N     j ^

Resposta

Primeira figura:

F → 1 =   - 11,2   k N     i ^ - 17,3   j ^  

F → 2 = - 28,8   k N

Segunda figura:

F → 1 = 34,7   k N   i ^ - 17,7   k N     j ^

F → 2 = 11,2   k N     i ^ + 18,7   k N     j ^

Exercícios de Livros Relacionados

O pino A , que conecta a viga de aço de 200k g com centro de gravidade em G à coluna vertical, é soldado tanto à viga quanto à coluna. Para testar a solda, o homem de 80k g carrega a viga exercendo um
Um ex-aluno de mecânica deseja se pesar, mas tem acesso apenas a uma balança A com capacidade limitada a 100l b e um pequeno dinamômetro de mola B de 20l b . Com o equipamento mostrado, ele descobre i
A barra uniforme O C de comprimento L gira livremente em torno de um eixo horizontal através de O . Se a mola de módulo k não é esticada quando C é coincidente com A, determine a tensão T necessária p
A porta de carga para um avião de seção circular da fuselagem consiste na carenagem semicircular A B uniforme de massa m . Determine a compressão C na escora horizontal em B para manter a porta aberta
Determine as tensões nos cabos A B , A C e A D .