Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.9 - Ex. 13iii

Com a condição de que as barras da figura abaixo estejam em equilíbrio, determine a intensidade das forças F → i

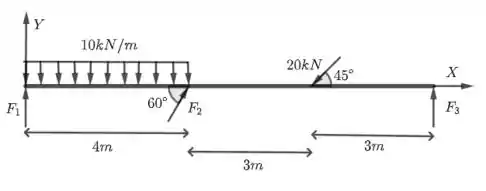
Passo 1

Temos 5 forças atuando nesse sistema. Começando pelas mais simples: F 1 → = F 1   j ^ e F 3 → = F 3   j ^ . F 2 → tem componentes

F → 2 =   F 2 c o s 6 0 °   i ^ + F 2   s e n   60 °   j ^ = 0,5   F 2   i ^ + 0,866   F 2     j ^

A força de 20   k N tem componentes:

F → 20 = -   20   k N c o s 45 °   i ^ - 20 k N     s e n   45 °   j ^ = -   20   k N ⋅ 0,707   i ^ - 20 k N   ⋅ 0,707   j ^

= - 14,1   k N   i ^ - 14,1   k N   j ^

Temos mais uma força de módulo 10   k N / m uniformemente distribuída de x = 0 até x = 4,0   m . Então, precisamos reduzir essa força:

R = ∫ 0 4 m p   d x = 10   k N / m ∫ 0 4 m   d x = 10   k N / m   ⋅ 4 m = 40   k N

∫ 0 4 m p x   d x = 10   k N / m   x 2 2 | 0 4 m = 10 k N / m   ( 4 m ) 2 2 = 10 k N / m ⋅ 8 m 2 = 80   k N m

⇒ x = ∫ 0 4 m p x   d x ∫ 0 4 m p   d x = 80   k N m 40   k N = 2 m

Assim, a força uniformemente distribuída é equivalente a aplicar uma força F → 40 = - 40   k N   j ^ no ponto x =   2 m .

Passo 2

Agora podemos aplicar as equações de equilíbrio

∑ F X = 0,5   F 2 - 14,1   k N = 0   ⇒ 0,5   F 2 = 14,1   k N ⇒   F 2 = 14,1   k N 0,5 = 28,2   k N

Já podemos aplicar F 2 = 28,2   k N diretamente na equação de equilíbrio para y :

∑ F Y = F 1 + F 3 + 0,866   F 2 - 14,1   k N - 40   k N = F 1 + F 3 + 0,866   ⋅ 28,2   k N - 14,1   k N - 40   k N

F 1 + F 3 + 24,4   k N - 14,1   k N - 40   k N = F 1 + F 3 - 29,7   k N = 0  

⇒ F 1 + F 3 = 29,7   k N

Passo 3

Temos duas incógnitas e somente uma equação. Isso quer dizer que precisamos utilizar a condição de equilíbrio para o momentos das forças ∑ M → = 0 . Para as forças que atuam perpendicularmente ao eixo x , os momentos serão somente a força multiplicada pela distância da mesma até a origem. Só precisamos prestar atenção ao sinal dos momentos, mas para isso utilizamos a regra da mão direita. Além disso, vamos calcular os momentos em relação à origem. Então

  • O momento da força F 1 → é nulo: M → 1 = 0
  • O momento da força F 3 → é M → 3 = 10 m   F 3   k ^
  • O momento da força F → 40 é M → 40 = - 40   k N   ⋅ 2 m   k ^ = - 80   k N m   k ^

Para as demais forças, temos:

  • r → 2 = 4 m   i ^ . Então

M 2 X = Y 2   F 2 Z - Z 2   F 2 Y = 0 - 0 ⋅ 0,866   F 2 = 0

M 2 Y = Z 2   F 2 X - X 2   F 2 Z = - 4 m ⋅ 0 = 0

M 2 Z = X 2 F 2 Y - Y 2   F 2 X = 4 m   ⋅ 0,866   F 2 - 0   ⋅ 0,5   F 2 = 3,64 m   F 2

  • r → 20 = 7 m   i ^

M 20 X = Y 20   F 20 Z - Z 20   F 20 Y = 0

M 20 Y = Z 20   F 20 X - X 20   F 20 Z = 0

M 20 Z = X 20   F 20 Y - Y 20   F 20 X = 7 m ⋅ ( - 14,1   k N ) - 0 ⋅ ( - 14,1   k N ) = - 98,7   k N m

Passo 4

Com todos os momentos das forças identificados, podemos utilizar a equação de equilíbrio para os momentos:

∑ M Z = 10 m   F 3 - 80   k N m + 3,64 m   F 2 - 98,7   k N m = 10 m   F 3 + 3,64 m   F 2 - 178,7   k N m = 0

⇒ 10 m   F 3 + 3,64 m   F 2 = 178,7   k N m   ⇒   F 3 + 0 , 364   F 2 = 17,87   k N

Agora temos um sistema de equações:

F 1 + F 3 = 29,7   k N

F 3 + 0 , 364   F 2 = 17,87   k N

Da segunda equação obtemos

F 3 = 17,87   k N - 0 , 364   F 2 = 17,87   k N - 0 , 364 ⋅   28,2   k N = 17,87   k N   - 10,26   k N = 7,61   k N

que podemos substituir na primeira:

F 1 = 29,7   k N - F 3 = 29,7   k N - 7,61   k N ≈ 22,1   k N

Resposta

F 1 = 22,1   k N

F 2 = 28,2   k N

F 3 = 7,61   k N

Exercícios de Livros Relacionados

A força P na alça da alavanca de posicionamento produz uma compressão vertical de 60l b na mola em espiral na posição mostrada. Determine a força correspondente exercida pelo pino em O na alavanca.
O cabo A B passa sobre a pequena polia ideal C sem uma alteração em sua tensão. Qual comprimento de cabo C D é necessário para equilíbrio estático na posição mostrada? Qual é a tensão T no cabo C D ?
A barra esguia e uniforme de comprimento 2 r e massa m repousa contra a superfície circular, conforme mostrado. Determine a força normal no pequeno rolo A e a magnitude da reação de pivô ideal em O .
A localização indicada do centro de gravidade da caminhonete de 3600l b é para a condição sem carga. Se uma carga cujo centro de gravidade está atrás do eixo traseiro for adicionada ao caminhão, deter
Calcule a magnitude da força suportada pelo pino em A sob a ação da carga de 1,5k N aplicada ao suporte. Despreze a fricção na ranhura.