Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 80

Determine a posição e para a aplicação da força P de modo que a viga sofra deflexão para baixo sem torção. Considere h = 200   m m .

Passo 1

Dados da questão: h = 200 m m ,   h 2 = 100   m m ,   b = 300   m m

A questão pede o centro de cisalhamento: e = ?

OBS: Esta questão é muito semelhante à Questão 7.72

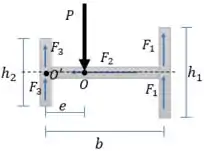
Para calcular o centro de cisalhamento vamos integrar o fluxo de cisalhamento sobre a viga para determinar as forças internas em função de P . Depois vamos fazer um cálculo de momento equivalente, para determinar a distância e .

Como já conhecemos a força que atua no ponto O (que é o próprio P ), então vamos fazer este cálculo de momentos em relação ao ponto O ' . Dessa forma não vamos precisar calcular as forças F 2 e F 3 .

Passo 2

Começamos calculando o momento de inércia

I = 1 12 t ⋅ h 3 + 1 12 b ⋅ t 3 + 1 12 t ⋅ h 2 3

Observe que t é a espessura de uma parede fina. Isso quer dizer que t é muito menor que as outras dimensões. Em outras palavras:

t 2 → 0

t 3 → 0

Com isso podemos simplificar a expressão:

I = 1 12 t ⋅ h 3 + 1 12 t ⋅ h 2 3

Chegamos numa expressão para o momento de inércia.

I = t 12 ( h 3 + h 2 3 )

Passo 3

Vamos uma expressão pro momento estático:

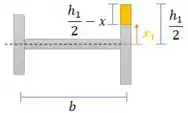
O momento estático é:

Q 1 = h 2 - x 1 ⋅ t ⋅ x 1 + h 4 - x 1 2

Q 1 = h 2 - x 1 ⋅ t ⋅ x 1 2 + h 4

Q 1 = t 2 h 2 - x 1 ⋅ h 2 + x 1

Chegamos numa expressão pro momento estático.

Q 1 = t 2 h 2 4 - x 1 2

Observe que para esse momento estático 0 < x 1 < h 1 , pois a aba tem tamanho h !

Passo 4

Para encontrar a força sobre a aba basta integrar o fluxo de cisalhamento:

F 1 = ∫ h 0 q 1 ⋅ d x  

F 1 = ∫ h 0 V Q 1 I ⋅ d x  

A força cortante é igual à força aplicada V = P

F 1 = ∫ h 0 P Q 1 I ⋅ d x  

F 1 = P I ∫ h 0 Q 1 ⋅ d x  

Substituindo o momento estático

F 1 = P I ∫ h 0 t 2 h 2 4 - x 1 2 ⋅ d x  

Efetuando a integral:

F 1 = P t 2 I ⋅ h 2 4 x 1 - x 1 3 3 h 1 0    

F 1 = P t 2 I ⋅ - h 3 4 + h 3 3    

Chegamos numa expressão para força na aba:

F 1 = P t 24 I ⋅ h 3    

Passo 5

Agora vamos calcular o somatório de momentos em O '

∑ M O ' = 0 ⇒ - 2 F 1 ⋅ b + P ⋅ e = 0

e = 2 F 1 b P

Substituindo F 1 :

e = 2 b P ⋅ P t 24 I ⋅ h 3

e = 2 t b 24 ⋅ 1 I ⋅ h 3

Substituindo o momento de inércia:

e = 2 t b 24 ⋅ 12 t ( h 3 + h 2 3 ) ⋅ h 3

e = b h 3 ( h 3 + h 2 3 )

Simplificando:

e = b 1 + h 2 3 / h 3

e = 266,67   m m

Resposta

e = 266,67   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga com o carregamento indicado, considerar a seção n - n e determinar: (b) a tensão de cisalhamento no ponto a .
Para a viga de perfil de aço laminado com abas largas e submetidas ao carregamento indicado, determinar numa seção localizada no meio do vão: (b) a maior tensão de cisalhamento, usando a aproximação τ
Para a viga de perfil de aço laminado com abas largas e submetidas ao carregamento indicado, determinar numa seção localizada no meio do vão: (a) a maior tensão normal.
Para a viga de perfil de aço laminado com abas largas e submetidas ao carregamento indicado, determinar numa seção localizada no ponto médio entre os pontos D e E : (b) a maior tensão de cisalhamento,
Para a viga de perfil de aço laminado com abas largas e submetidas ao carregamento indicado, determinar numa seção localizada no ponto médio entre os pontos D e E : (a) a maior tensão normal.