A viga é apoiada por um pino em e um elo curto . Se , determine a tensão de cisalhamento média desenvolvida nos pinos em . Todos os pinos estão sujeitos a cisalhamento duplo, como mostra a figura, e cada um tem diâmetro de
Passo 1
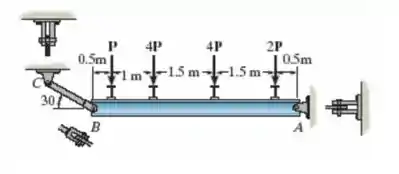
Primeiramente constatamos que o comprimento da viga é a soma de todas as cotas dadas no enunciado, assim teremos: . Além disso, podemos fazer o seguinte diagrama de forças para o problema
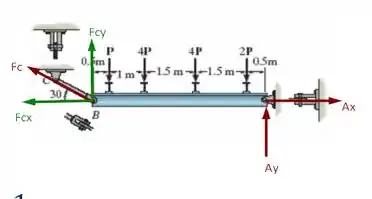
Onde a força pode ser decomposta em duas componentes: uma vertical e uma horizontal que foram desenhadas em verde no nosso diagrama. Assim, pela decomposição de vetores temos
Passo 2
Feitas as considerações iniciais podemos ir para o somatório das forças nas direções que nos forem convenientes. Dessa forma vamos ter
Adotando o sentido horário como positivo temos
Como temos apenas e fazendo força para cima e temos para baixo, descoberto o valor de podemos concluir que . Agora, com as equações da decomposição de vetores teremos
Passo 3
Por fim, podemos calcular as tensões de cisalhamento lembrando que como todos os pinos sofrem cisalhamento duplo devemos dividir as forças por 2, assim
Para os pinos B e C:
Já para o pino A vamos calcular primeiramente a força que está provocando o cisalhamento que vai ser exatamente a resultante de , calculada como
Então