Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 9.Problemas de Revisão - Ex. 160
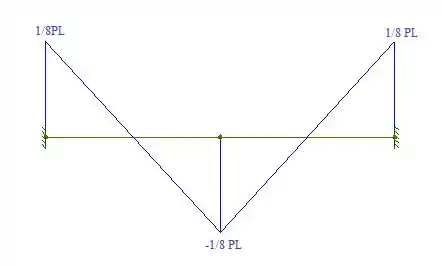
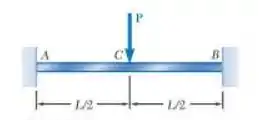
Determine a reação em e desenhe o diagrama de momento fletor para a viga e o carregamento mostrados nas figuras.
Passo 1
Fala aí, galera. Tudo bem? Bora pra outra questão.
Primeiramente, precisamos da equação do momento na estrutura. Primeiro, vamos determinar as reações de apoio através das equações de equilíbrio. Por simetria, temos que:
Portanto:
Em seguida, vamos determinar o momento para o segmento :
Agora, com a equação do momento encontrada, basta substituir na equação da linha neutra e integrar duas vezes para acharmos a equação da linha elástica. Logo:
Passo 2
Com as equações acima, basta aplicar as condições de contorno. Sabemos que:
Agora, basta substituir nas fórmulas para achar as constantes. Fazendo isso:
Assim, podemos encontrar os momentos nos 3 pontos. Por simetria:
Portanto, dado que nestas condições não há inclinação nas extremidades, temos que:
E também, no ponto médio, a inclinação é nula no ponto , logo:
Assim, podemos esboçar o diagrama de momento fletor. Fica assim:
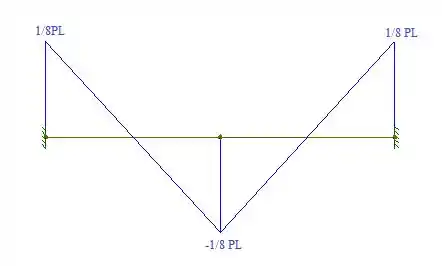
Resposta
