Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 96
Se , determine a reação , a reação .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
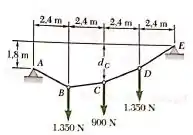
Temos o seguir o diagrama de corpo livre:
Calculando o momento no ponto , temos:
Passo 2
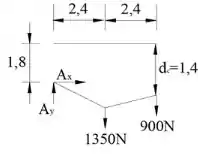
A próxima equação para determinar a reação no ponto é obtida através do diagrama de corpo livre no cabo , mostrado a seguir:
Fazendo o somatório de momentos no ponto , podemos determinar a próxima equação para determinara a reação no ponto :
Como descobrimos que:
Então vamos substituir:
Resolvendo, temos que:
Portanto:
Passo 3
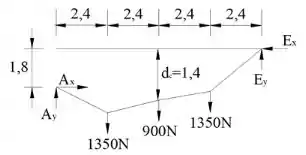
Fazendo o somatório de forças em para o sistema, temos:
Fazendo o somatório em , temos:
Passo 4
Agora que temos as componentes é só aplicar Pitágoras para descobrir o valor da reação.
E:
Resposta
Exercícios de Livros Relacionados
(a) Determine o vão horizontal máximo permitido para um cabo uniforme de peso por unidade de comprimente w se a tração no cabo não exceder um valor dado T m (b) Usando o resultado da parte a , determi
Para a viga e o carreamento mostrados nas figuras, a Trace os diagramas de esforço cortante e de momento fletor, b determine os valores absolutos máximos do esforço cortante e do momento fletor..
Para a viga e o carreamento mostrados nas figuras, a trace os diagramas de esforço cortante e de momento fletor, b determine a intensidade e a localização do máximo valor absoluto do momento fletor.
Para a viga e o carreamento mostrados nas figuras, a Trace os diagramas de esforço cortante e de momento fletor, b determine os valores absolutos máximos do esforço cortante e do momento fletor..
Para a viga e o carreamento mostrados nas figuras, a trace os diagramas de esforço cortante e de momento fletor, b determine a intensidade e a localizaão do momento fletor máximo.