Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 5.Problemas fundamentais - Ex. 8
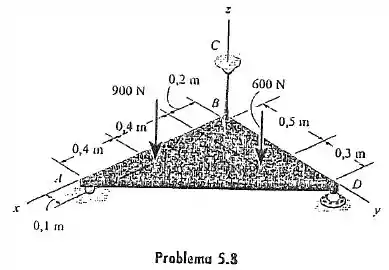
Determine as reações no apoio de rolete e na junta esférica e determine a tração no cabo para a placa.
Passo 1
Vamos lá pessoal! Queremos as reações em e .
Como é um cabo, a reação dele é só uma força vertical. Já em temos um rolete, esse cara nos dá só uma reação vertical também. Já a junta esférica em vai dar reações nas nossas três direções.
Para trabalhar esta questão vamos desenhar o diagrama de corpo livre da nossa situação, para ficarmos ligados no que temos que trabalhar:
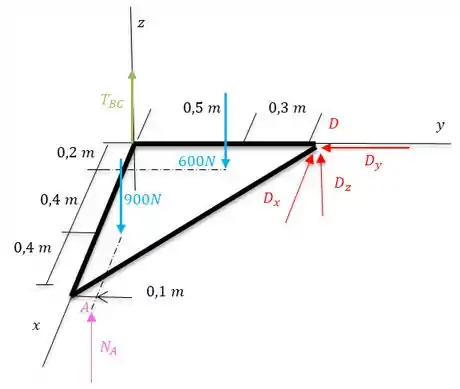
Para termos um bom raciocínio aqui, é muito bom pensarmos apenas por eixos isso facilitará a resolução.
Passo 2
Bem, olhando a imagem fica claro, o rolete só apresenta reação normal a força. Partiu determinar essa normal.
Vamos olhar o momento em relação ao eixo , porque as reações do cabo e da esfera não geram momento nele. Para a situação de equilíbrio do sistema, o somatório do momento em relação a um ponto é igual a zero. Assumindo o sentido anti-horário como positivo, temos:
Isolando , fica:
Passo 3
Vamos trabalhar agora com as reações da nossa junta esférica .
Note que pelo nosso desenho temos que determinar reação em todos os eixos.
Vamos começar com :
Vamos calcular o momento em relação ao eixo , isso porque não causa momento nele. Novamente estamos em uma situação de equilíbrio, portanto, o somatório do momento deverá ser igual a zero.
Considerando o sentido anti-horário como positivo, temos:
Isolando :
Passo 4
Para determinarmos o restante das componentes de , vamos analisar o somatório de forças em cada uma das coordenadas.
Novamente estamos em situação de equilíbrio.
A única força atuando no eixo é . Portanto:
O somatório de forças em no eixo :
A unida força atuando no eixo é . Portanto:
Passo 5
Para determinar a tensão no cabo , perceba que a tensão se encontrar no eixo , logo, vamos executar o somatório de forças no eixo .
Assumindo a direção para cima como positivo.
Lembrando estamos em equilíbrio.
Isolando :
Resposta
Reação do rolete:
Reação da junta esférica:
Tensão no cabo: