Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 121

Determine as reações nos apoios A e B . E I é constante.

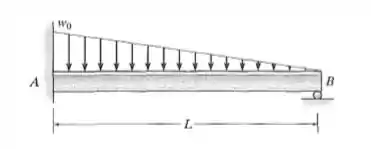
Passo 1

Fala aí pessoal, partiu mais um problema de resmat. Este problema pede as reações de apoio e os diagramas. A dificuldade está em encontrar as reações de apoio, pois é uma estrutura hiperestática. Primeiro, vamos fazer o DCL:

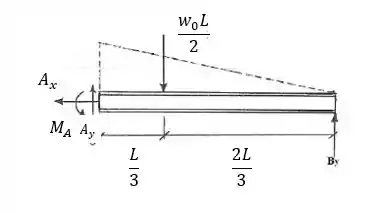
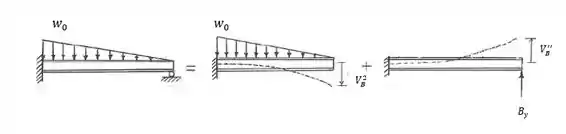
Passo 2

Agora vamos utilizar as equações de equilíbrio e momento para determinarmos as reações:

sum M_A = 0 M_A - ((w_0 L)/(2)) ((L)/(2)) + B_y L = 0 M_A = (w_0 L^2)/(6) - B_y L

sum F_y = 0 A_y + B_y - (w_0 L)/(2) = 0 A_y = (w_0 L)/(2) - B_y

sum F_x = 0 A_x = 0

Passo 3

Por fim, temos:

v_B^' = - (w_0 L^4)/(30 E I)

V_B^(' ') = (P L^3)/(3 E I) = (B_y L^3)/(3 E I)

Sabendo a equação de compatibilidade , vamos substituir:

V_B^' + V_B^(' ') = 0 - (w_0 L^4)/(30 E I) + (B_y L^3)/(3 E I) = 0 B_y = (w_0 L)/(10)

Substituindo nas equações obtidas anteriormente, encontraremos as rea��ões nos apoios restantes: A_y = (w_0 L)/(2) - B_y A_y = (2 w_0 L)/(5)

M_A = (w_0 L^2)/(6) - B_y L M_A = (w_0 L^2)/(15)

Resposta

A_x = 0

B_y = (w_0 L)/(10)

A_y = (2 w_0 L)/(5)

M_A = (w_0 L^2)/(15)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga é feita de um material elástico macio com EI constante. Se ela estiver originalmente à distância ∆ da superfície do apoio de sua extremidade, determine a distância a à qual a extremidade da vig
A estrutura em caixão é submetida a uma carga uniformemente distribuída w ao longo de cada um de seus lados. Determine o momento desenvolvido em cada canto. Despreze a deflexão provocada pela carga ax
Determine as reações em A e B . Considere que o apoio em A exerce somente um momento sobre a viga. E I é constante.
Cada um dos dois elementos estruturais é feito de alumínio 6061-T6 e tem seção transversal quadrada de 25m m ×25m m . Suas extremidades estão engastadas por pino, e um macaco é colocado entre eles e a
Determine as reações em A e B . Considere que o apoio em A exerce somente um momento sobre a viga. E I é constante.