Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 3.Problemas de Revisão - Ex. 2
Determine o máximo de massa do motor que pode ser suportada sem exceder uma tração de na corrente AB e na corrente AC.
Passo 1
Oi pessoal? Vamos para mais um exercício?
O primeiro passo é desenhar o diagrama de corpo livre do nosso sistema. Temos que:
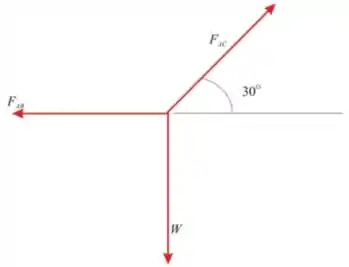
Passo 2
Para o eixo , temos que:
Assumindo que , teremos que:
Este valor é maior que e isto não é possível.
Assumindo agora que , temos que:
E este valor é possível.
Passo 3
Fazendo o somatório das forças em , temos que:
Substituindo os valores podemos obter o valor da massa do motor.
Resposta
Exercícios de Livros Relacionados
O caminhão é simetricamente apoiado no solo por duas extensões laterais em A e duas em B , descarregando sua suspensão e dando estabilidade contra o tombamento. Se o guindaste e o caminhão possuem mas
Determine a intensidade e a direção θ da força mínima P necessária para puxar o rolete de 50k g sobre o degrau liso
Determine as reações no elemento em “L” que é apoiado por uma superfície lisa em B e por uma luva em A , que está fixa ao elemento e livre para deslizar pela alça inclinada presa à parede.
Determine as reações que atuam sobre o elemento uniforme liso, que tem massa de 20 kg.
A lança apoia duas cargas verticais. Desconsidere o tamanho dos colares em D e B e a espessura da lança, e calcule as componentes horizontal e vertical da força no pino A e a força no cabo C B . Consi