Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 148
Resolva o Problema considerando que o ângulo formado pela barra e pela horizontal é .
Passo 1
Bom galera, vamos fazer um diagraminha de corpo livre, só pra facilitar nossa vida:
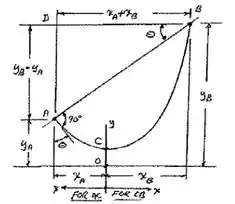
Com isso, de cara a gente já tem algumas informações:
Passo 2
Show de bola, vamos dar uma analisada no ponto :
E o comprimento do cabo é :
Passo 3
Calma, tá quase acabando. Vamos usar também a equação :
Onde temos em :
Montando um sistema com essas equações e o que já temos a gente consegue encontrar:
Passo 4
Por fim, aplicando de um por um nas equações, encontraremos:
E assim:
Resposta
Exercícios de Livros Relacionados
Um cabo tem massa por unidade de comprimento de 3k g / m e é erguido tal como mostra a figura. Sabendo que L é 6m , determine os dois valores da flecha h para os quais a tração máxima é 350N .
Sendo θ o ângulo formado entre um cabo uniforme e a horizontal, mostre que, em qualquer ponto, (a) s = c tan θ , (b) y = c sec θ .
Determine a razão flecha por vão para a qual a tração máxima no cabo é igual ao peso total do cabo A B interno.
Um cabo A B de 3m é fixado em dois colares como mostra a figura. O colar em A pode deslizar livremente ao longo da haste; um batente de fixação na haste evita que o colar B se mova na haste. Desprezan
À esquerda do ponto B , o cabo longo A B D E repousa sobre a superfície horizontal áspera mostrada na figura. Sabendo que a massa por unidade de comprimento do cabo é 2k g / m , determine a força F qu