Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.6 - Ex. 78
Determine a resultante das quatro forças atuando na placa de união. Ache também o módulo de e o ângulo que a resultante faz com o eixo .
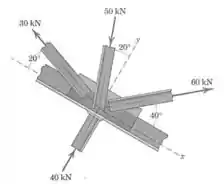
Passo 1
A forma mais fácil de calcular a soma vetorial dessas quatro forças é encontrar as componentes de cada uma nos dois eixos.
Começamos com as componentes na direção , lembrando de ajustar os sinais em cada uma:
E agora fazemos a mesma coisa para as componentes na direção :
E então o vetor é:
Passo 2
Agora precisamos calcular o módulo desse vetor:
E para encontrar o ângulo que que ele forma com o eixo só precisamos usar a definição da tangente:
Resposta
O vetor é , que tem módulo e o ângulo é .
Exercícios de Livros Relacionados
Se F = 200N , determine o ângulo exigido θ , de modo que o momento de binário resultante seja zero. O disco tem um raio de 300m m .
Um momento de 4N ⋅ m é aplicado ao cabo da chave de fenda. Decomponha esse momento de binário em um par de forças de binário F exercidas sobre o cabo e P exercidas sobre a ponta da chave.
Um binário no sentido horário M = 5N ⋅ m é resistido pelo eixo do motor elétrico. Determine a intensidade das forças reativas - R e R que agem nos suportes A e B , de modo que a resultante dos dois bi
O homem tenta abrir a válvula aplicando as forças de binário de F = 75N ao volante. Determine o momento de binário produzido.
Se a válvula puder ser aberta com um momento de binário de 25N ⋅ m , determine a intensidade exigida de cada força de binário que deve ser aplicada ao volante.